A peer-reviewed electronic journal published by the Institute for Ethics and
Emerging Technologies

ISSN 1541-0099

28(1) – December 2018

Forever and Again:

Necessary Conditions for “Quantum Immortality” and its Practical Implications

Alexey Turchin

Science for Life Extension Foundation

Digital Immortality Now

alexeiturchin@gmail.com

Journal of Evolution and Technology - Vol. 28 Issue 1 – December 2018 - pgs 31- 56

Abstract

This article explores theoretical conditions necessary for “quantum immortality” (QI) as well as its possible practical implications. It is demonstrated that QI is a particular case of “multiverse immortality” (MI), which is based on two main assumptions: the very large size of the universe (not necessarily because of quantum effects); and a copy-friendly theory of personal identity. It is shown that a popular objection about lowering of the world-share (measure) of an observer in the case of QI does not succeed, as the world-share decline could be compensated by merging timelines for the simpler minds, and because some types of personal preferences are not dependent on such changes. Despite large uncertainty about the truth of MI, it has appreciable practical consequences for some important outcomes like suicide and aging. The article demonstrates that MI could be used to significantly increase the expected subjective probability of success of risky life extension technologies, such as cryonics, but that it makes euthanasia impractical because of the risk of eternal suffering. Euthanasia should be replaced with cryothanasia, i.e. cryopreservation after voluntary death. Another possible application of MI is as a last chance to survive a global catastrophe. MI could be considered a Plan D for reaching immortality, where Plan A consists of survival until the development of beneficial Artificial Intelligence capable of fighting aging, Plan B employs cryonics, and Plan C is digital immortality.

Highlights

· Quantum immortality (QI) is a particular case of multiverse immortality (MI).

· The validity of MI depends on the size of the universe and the nature of personal identity, but is still uncertain.

· The counterargument of “world-share decline” depends on the type of preferences and merging timelines.

· MI greatly increases the subjective chances of the success of cryonics, makes euthanasia impossible, but favors cryothanasia.

· MI is our last line of defense against existential risks.

Disclaimer: Suicide will never be useful as an implication of QI: if QI is true, suicide will probably result in a non-deadly serious injury, permanent brain damage, and infinite suffering. Accordingly, the idea of QI is not an argument for suicide, but is one of the strongest arguments against it. If you are interested in suicide, seek professional psychological help.

Warning: Memetic hazard for people who tend to react emotionally to thought experiments!

Abbreviations

AI – Artificial Intelligence

QS – Quantum suicide (or quantum suicide thought experiment)

QI – Quantum immortality

MI – Multiverse immortality: umbrella term for QI and big world immortality

MWI – Many-worlds interpretation of quantum mechanics

UDT – Updateless Decision Theory

1. Introduction

The main idea behind quantum immortality (QI) is that constant branching of the multiverse – according to the many-worlds interpretation (MWI) of quantum mechanics – ensures the existence of timelines in which a given observer will survive any dangerous situation. The idea was suggested in the form of a quantum suicide (QS) thought experiment by Tegmark (1998) and others.

Most scientists who have written about the idea of QI have felt an obligation to disprove it (Randall 2004; Mallah 2009; Almond 2011a; Aranyosi 2012),¹ in the same way as most authors try to disprove the notorious Doomsday argument (Bostrom 1999), which is commonly interpreted as supporting a pessimistic estimate of how long humanity will survive as a species. Critics of QI do not analyze the implications if QI is true, and as result, the possible practical consequences of the idea are underexplored.

Quantum immortality is closely related to the effective altruism circle of problems. If QI is real, it follows that there is a possibility of infinite future suffering for any sentient being (Aranyosi 2012), as it will not be able to die, but will continue to age. So, QI is an s-risk. The concept of an s-risk was introduced by Max Daniel (2017) to denote risks whose outcomes could include “suffering on an astronomical scale, vastly exceeding all suffering that has existed on Earth so far.”² In what follows, however, it will be demonstrated that there is a way to prevent this s-risk for people who are currently alive. This involves increasing their possible positive timelines, extending into the infinite future, by signing up to cryonic suspension and storage.³

An overview of the history of the idea of QI, its formalism, and its relation to the idea of death is presented in Section 2. Section 3 is devoted to the difference between QI and multiverse immortality (MI), and the conditions necessary for them to be true are analyzed. Section 4 explains the possible bad consequences of “natural” QI. In Section 5, QI is explored from the point of view of decision theory, and the “measure decline” objection is analyzed. Section 6 provides an overview of the practical applications of QI, including overcoming the negative effects of natural QI via cryothanasia (cryopreservation after voluntary death).

2. The nature and formalism of multiverse immortality

2.1 History of the idea

The first stage of the concept that the infinite size of the universe implies some form of immortality was the idea of so-called eternal return, that is, the repeated appearance of the same observers. The earliest versions of the eternal return theory appeared in ancient philosophy (Eliade 1949) and still attract interest today (Bergström 2012). Empedocles of Akragas reportedly believed in the cyclic return of everything based on the recombination of four elements, ensuring personal immortality (Brown 1984).

In more recent thought, the idea that an infinite universe implies some form of immortality came to Romantic poet Heinrich Heine in the first half of the nineteenth century. He wrote:

For time is infinite, but the things in time, the concrete bodies, are finite. They may indeed disperse into the smallest particles; but these particles, the atoms, have their determinate number, and the number of the configurations that, all of themselves, are formed out of them is also determinate. Now, however long a time may pass, according to the eternal laws governing the combinations of this eternal play of repetition, all configurations that have previously existed on this earth must yet meet, attract, repulse, kiss, and corrupt each other again. (Kaufmann 2013, 318)

The idea of “cyclic immortality” was postulated by French socialist Louis Blanqui in his book Immortality Through the Stars (1872). Friedrich Nietzsche arrived at the same idea, his famous theory of eternal return or eternal recurrence, in the 1880s: he recorded in his notes that it first occurred to him in August 1881, and he published the idea in 1882, in the first edition of The Gay Science. Subsequently, it became a central idea in Thus Spoke Zarathustra (originally published 1883–1891), in which acceptance of the possibility of eternal recurrence is a defining feature of the Übermensch. However, Nietzsche either did not understand or ignored the obvious consequence of eternal recurrence, that there will always be a world, similar to our world until the moment of the observer’s death, but different in the moment of the death in such a way that the observer will not die. This implies immortality from the subjective view of any observer. Thus, the idea of MI (of which QI is an important specific case) is a natural development of Nietzsche’s idea.

Hugh Everett, working on quantum mechanics in the middle of the twentieth century, was probably the first person to come to the idea that a constantly branching universe implies immortality from the subjective point of view, based on his discovery of MWI as an interpretation of quantum mechanics. However, he never stated this conclusion publicly (Shikhovtsev 2003). It was only at the end of the twentieth century that the key idea for current purposes – that the existence of the multiverse implies some form of immortality – became known as “quantum immortality” following the “quantum suicide” (QS) thought experiment proposed by Moravec (1988), Marchal (1991), and Squires (1994), and later popularized by Tegmark (1998).

The preservation of information implicit in quantum mechanics, and known as the “no-hide theorem” (Braunstein and Pati 2007), is not connected with the idea of QI as it was originally presented by Tegmark and others. In the original QI theory, human survival happens in only one of the branches of the quantum multiverse, and preservation of the information in other branches is not necessary. However, such quantum preservation could be used by another approach to the resurrection of the dead, i.e. “quantum archeology,” which is out of the scope of this paper, but has been addressed elsewhere by the author (Turchin and Chernyakov 2018) and by Jonathan Jones (2017).

Previous work has sought to identify the truth or falsity, and the practical features, of QI, but the idea has only a few vocal proponents. In the 1990s, Higgo (1998) tried to present QI as a legitimate theory of immortality, but his analysis is not deep. About the same time, Robert Charles Wilson explored the possible consequences of quantum immortality in his short story “Divided by Infinity” (first published in 1998 in the anthology Starlight 2, edited by Patrick Nielsen Hayden), in which the protagonist survives multiple suicide attempts (and even a global catastrophe) and is resurrected by aliens.

Allan F. Randall (2004) criticizes QI from the point of view that its most likely outcome is neither “technological resurrection” nor “eternal decrepitude,” but chaotic random observers similar to Boltzmann brains. He does, however, note the usefulness of QI for cryonics. Brett Bevers (2011) explores how QI relates to the Born rule, a central principle in quantum mechanics, and apparently breaks it. Milan M. Ćirković (2006) correctly mentions that a theory of personal identity is critical for QI, and proceeds to prove that, in the case of QI, subjective credence should be equal to the objective probabilities. Paul Almond (2011) extensively criticizes the idea that the QS thought experiment could be used as a proof of MWI. Elsewhere (Almond 2008), he suggests that QS could be a “universal problem solver,” and that the concept of civilizational-level QS could be used to explain the Fermi paradox.

Greg Egan’s idea of “dust theory” (see Egan 2009)⁴ seems to be the next step in developing the idea of QI, similar in significance to the step from the eternal recurrence in the nineteenth century to the late-twentieth-century QS thought experiment. In dust theory, something similar to QI happens in every observer-moment; such moments could exist completely separately from each other, as random patterns in infinite “dust,” or as Boltzmann brains, but could look subjectively connected “from inside” based on their similarity. An important conclusion of such a theory is that there is no need for an external reality other than the unstructured and endless dust, and that each observer-moment could have many pasts and many futures. The mathematical theory of such a world was recently suggested by Marcus P. Müller (2018). The truth or otherwise of such récherché theories is, however, out of the scope of this paper; rather, the actual existence of an objective and structured world, governed by observer-independent laws of physics, is assumed throughout.

Christian Loew (2017) has suggested an idea similar to Egan’s dust theory, that of “Boltzmannian immortality,” which is basically a reincarnation of the eternal return that takes into account Boltzmann brains randomly appearing from vacuum if an empty universe lasts for an infinitely long period.

2.2 The quantum suicide thought experiment and infinite survival timelines

The main idea of the QS thought experiment is that a quantum event, such as radioactive decay of an atom, will trigger a powerful bomb near me, an observer, with a probability⁵ of 0.5. In such a situation, two future timelines are possible, depending on whether or not the bomb explodes. If MWI is true, both timelines are real. In one, I continue to exist, and in the other I am instantly destroyed. Thus, I will observe only the timeline in which the bomb didn’t explode. This experiment seems similar to the famous thought experiment involving Schrödinger’s cat, but without the tantalizing idea that the observer could be in a superposition of dead and alive states.

Thus, QS entails that an observer will always observe a winning result in Russian roulette, which may seem (to them) as if they have surprising skills of survival. The main question is whether the inevitable observation of not dying in such an experiment can be equated to subjective immortality: in MWI, there will always be a timeline in which the bomb didn’t explode after any number of attempts – but is this enough to conclude that the observer is immortal?

The QS thought experiment has also been analyzed as a possible proof for MWI: how many failed attempts at suicide are enough for an observer to conclude that the MWI is true? Almond and others have invested significant time in proving that no number of instances of survival in QS could be a proof of MWI. However, as Bostrom notes (2002), if observations are discarded based on the assumption that in an infinite universe there exists an observer for any possible observation, science is not possible as observation loses its predictive power.

While QS requires exotic devices, such as a bomb and a quantum random generator, there is no reason to think that any ordinary cause of death is different. Dying will be more complex, but eventually there will be two main types of future timelines: those in which I died and those in which I survived. However, slower dying implies some more complex dynamic, such as an increased probability of survival in an injured state that includes suffering. This will be addressed later.

In a nutshell, QS entails some form of QI – “quantum immortality” – i.e., for any observer, there is (at least one) infinite future timeline in which that observer will continue to exist. However, as will be shown in the next section, such a result could happen not only in a quantum world, but even in a completely classical world, if some conditions held relating to the world’s size and the observer’s internal structure.

2.3 Formalism of multiverse immortality

One useful instrument when speaking about observers is the idea of “observer-moments,” that is, the shortest periods of subjective experience, probably corresponding to one step of the internal human clock (which has a duration of a few tens of a millisecond). For simplicity’s sake, it is assumed here that any observer-moment is characterized by the name I and a time-stamp t, and the observer-moment is thus notated as O(I, t). Then, immortality can be defined as the following statement: For any observer-moment O(I, t) there necessarily exists (at least one) observer-moment O(I, t+1). The following is immediately implied: There is no last observer-moment O(I, t_last), so there is no death.

Note that there is a hidden claim that the existence of O(I, t+1) is sufficient for immortality. This exact claim typically raises the most objections: while some might agree that somewhere in the multiverse there exists a copy of me which survived my death, they claim that such existence is not immortality qua immortality because of a different identity, or lower “measure,” or some decision-theoretic considerations. Some of these objections will be discussed in the sections that follow.

The definition of immortality involved here is general and – hypothetically – could be satisfied through many conceivable processes (e.g. God created the world this way). What is claimed in MI theory is that the infinitely large size of the universe is sufficient to satisfy the immortality definition (given a few other assumptions).

2.5 The logical indefinability of the observer’s death

There is a well-known conjecture that is expressed in the following syllogism: “All humans are mortal (i.e. will die), I am a human, so I am mortal (i.e. I will die).” Though it is well-known, it has several flaws. One is the “fallacy of four terms” (Copi and Cohen 1990), as the concept of mortality (and hence of death) has different meanings in the first premise of the syllogism and in its conclusion. In the premise, the concept of death is “death-for-others”, i.e. observation of death by outside observers, or cessation of the living activity of the body. In the conclusion, the concept of “death-for-me” is used, which means the death of the observer from the observer’s point of view, typically expressed by the idea of “nothingness after death” or cessation of the process of observation. However, by definition, no one can experience and report anything about nothingness after death, so it is not possible to prove that it will actually happen.

Multiverse immortality means that death – from the observer’s point of view – is impossible. In other words, for any state of any observer with time-stamp t₀, there is a possible next state t₀+1, and, as everything possible exists, such an observer exists. Thus, a last moment of experience is impossible, and death – as the cessation of the process of experiencing – is impossible. Almond (2011b) attacks this idea and notes that if MWI is not true, the death of the observer is a consistent explanation of reality, but if it is assumed that the MWI is true, death in some branches immediately becomes an inconsistent explanation. According to Almond’s work, this jump between varying descriptions of death is not logical and undermines the idea of QI. In other words, if it is agreed that death is theoretically possible, because of a small world, it should also be agreed that death is possible in the branching world, in the form of the death of some branches. This is not a question of fact, but one of interpretation: should the continued existence of a person’s quantum duplicate (or some other kind of copy) be regarded as immortality or not?

The answer to the problem raised by Almond is connected with the nature of personal identity, which will be analyzed in the next section. If identity is connected with the measure of existence, then there is some probability that lowering this measure is equal to death. If identity depends only on information, then a change in the number of copies is irrelevant. The nature of death depends on the nature of personal identity, and death could be described as “the end of identity.” Another counterargument is that if I am not currently on Mars, that doesn’t mean that I am dead on Mars. In any given moment, there are a lot of branches which are not happening with me, but it doesn’t mean that I die every moment – and if the non-existence of a branch is considered a death, I am dying every second in millions of ways.

2.6 Examples of multiverse immortality

There is nothing strange in the idea of MI, when simpler objects and beings are considered:

Numbers are immortal. All numbers appear over and over again in multiple worlds, and it could be said that any given number is “immortal.” In principle, the same is true for number series: the number 27 will appear again and again, but we are not surprised by this, as the number is small compared to the size of our world, where we can find, for example, 27 ships and 27 sheep. The repetition of longer numbers in the world becomes more and more surprising – but only because the world seems to be too small for such repetition. In an infinitely large and random world, any number or series of numbers will repeat.

Simple molecules are immortal. A molecule of water will appear again and again, because it is very simple, and consists of abundant components. But more complex compounds are rare. Some short organic molecules are likely to repeat rather often, while a molecule with around 100 randomly connected atoms will be so rare that it might appear only once in our Hubble volume. In other words, the simpler the object, and the more stochastic its environment, the more likely it will possess something like MI.

Biological viruses. Even some living beings could enjoy this type of immortality in an observable way. Biological viruses of one species are all functionally equivalent to each other (barring mutation) and the death of one copy is not the death of the virus.

2.7 Overview of the types of multiverse immortality

“Multiverse immortality” – MI – will be used in what follows as a general term that unites three subtypes. However, these subtypes may have no observational differences: eternal return will look like QI if someone’s life history completely repeats in the future until the moment of death, but, in that moment, becomes different – and the only difference is that the person will not die. All three types are identified in Table 1 below and depicted pictorially in Figures 1–3.

A useful metaphor to understand MI is the thought experiment that provides the basis of Jorge Luis Borges’ short story “The Library of Babel” (originally published in Spanish, 1941; English translation 1962). In the library of Babel, an infinite number of copies of all possible books exists. If one copy of a book disappears, the book still exists within the library, maybe different in just a few typographical errors.

In passing, it should be noted that a different meaning of the term “quantum immortality” is sometimes discussed. In this sense, QI is a form of near-death experience after which a person jumps backward to an earlier point in their life and relives the moment of a dangerous situation (typically, a car accident) without dying.⁶ While some people do have this experience as a hallucination, it is not the original idea of QI, which cannot be reported to outside observers, and in which there are no temporal jumps. Quantum immortality does not require a “quantum mind” or other quantum woo: it is based solely on MWI, a scientifically respected interpretation of quantum mechanics. It does not require any quantum effects except the existence of observer copies in other branches of a multiverse.

Table 1. Types of multiverse immortality

	Subtype	Underlying properties of the multiverse
Multiverse immortality	Eternal return with alternative ending	Infinite in time
	Big world immortality	Infinite in space or parallel worlds
	Quantum immortality	Many-worlds interpretation of quantum mechanics

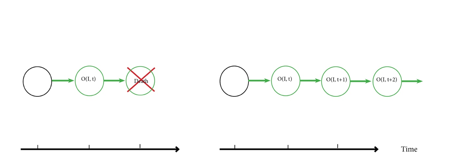
Figure 1. Eternal return with an alternative ending at the moment of death.

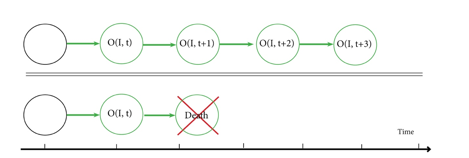
Figure 2. Big world immortality. There is another copy of an observer in a causally disconnected region of the universe, and this observer-copy does not die at the moment of the observer’s death.

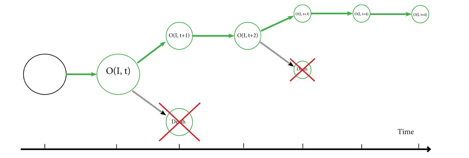Figure 3. Quantum immortality. There is always a branch of the multiverse in which the observer does not die. Smaller circles represent “measure decline;” the green line indicates the timeline of survival.

3. Necessary conditions for multiverse immortality: The huge size of the universe and a “copy-friendly” theory of personal identity

Two conditions are essential for MI: that there exists an infinite number of copies of an observer with alternative life histories, and that the replacement of an observer with its exact copy is a sufficient condition for immortality.

The first condition is factual: it is a claim that the universe is built in such a way that, for any situation in which an observer has died, there exists another copy of the same observer who lived through that exact moment. Note that this condition is realized by different physical mechanisms for QI and for big world immortality. In the first case, however, it is realized via branching of the world wave function, while in the second case, the universe is so large that such copies will appear in it because of combinatorial effects. While the mechanisms are different, the result is the same: infinitely many copies ensure the existence of endless chains of observer-moments.⁷

The second condition is not a factual claim, but a decision-theoretic one; it states that an individual should act as if she is immortal after she learns the first factual condition (and assuming some type of subject-centered preferences). Both conditions will be explored in detail in this section.

3.1 Condition 1: Repetition of human minds in the universe

3.1.1 Tegmark’s levels of multiverse

Max Tegmark (Tegmark 2009) identified four levels of the multiverse sufficient to create a world large enough to include all possible observers’ minds, at least those the size of a human mind. These are as follows:

Level 1. Regions beyond our cosmic horizon, that is the very large size of our own bubble. “A generic prediction of cosmological inflation is an infinite ‘ergodic’ space, which contains Hubble volumes realizing all initial conditions — including an identical copy of you about 10¹⁰^²⁹ m away” (Tegmark 2009). The scale of chaotic inflation is supported by observations of anisotropy. One estimate is 10^{^{10^{10^{122}}}} megaparsecs (Page 2007).

Level 2. Other post-inflation bubbles. Quantum foam during the Big Bang creates many bubbles with differing laws of physics. Their existence is supported by ideas that fine-tuning of physical laws is explained by the observer selection effect, also known as the anthropic principle.

Level 3. Many worlds interpretation of quantum mechanics.

Level 4. Mathematical universe: all possible mathematical structures exist. This is the most simple explanation of the fact that everything exists at all.

The first level is tentatively supported by data from contemporary cosmology, first of all, cosmological inflation, as explained by Tegmark. So, big world immortality in a very large universe receives even stronger scientific support than QI, which is based on an interpretation of quantum mechanics that currently remains untestable. However, all this evidence is indirect and is merely an extrapolation of our best theories of cosmology. Some other cosmological theories also allow MI, e.g. a cyclic universe, a spatially finite universe that exists for an infinitely long time via a series of Big Bangs and Big Crunches (Steinhart and Turok 2002), and a fecund universe that replicates via black holes (Smolin 1992).

The anthropic principle in a fine-tuned universe can also be regarded as evidence for a very large universe with a variety of possible physical constants (Bradley 2009), since numerous “attempts” are required to create the right combination. By some estimates, as many as 10⁵⁰⁰ instances might be required just to arrive at the optimal combination of physical constants.⁸ There are many cosmological theories, but it is not easy to create a viable cosmological theory that results in just one small universe that is fine-tuned for life; in a sense, it is computationally simpler to devise a process that creates all possible universes.

The more general argument for an infinite universe is philosophical. There is a process that makes the universe appear from “nothing,” as could be concluded from the fact of the universe’s existence. For a non-infinite universe, this process must stop at some point, preventing new universes from appearing. But stopping this process would require a force acting on nothingness, i.e. from beyond the universe. However, the universe is, by definition, the only thing which exists: there can be nothing beyond it. Thus, the process that created the universe cannot be exhausted. Approximately the same logic was presented by Kant in his Critique of Pure Reason (originally published 1781). Among Kant’s celebrated “antinomies,” was that relating to the finite or infinite extent of the universe in time and space, where both alternatives were said to be paradoxical. There is, however, a possible solution: that the universe is neither finite nor infinite, but is instead constantly growing.

One attractive property of Tegmark’s levels 1 and 2 is that they are only currently causally disconnected. They arose from the same causal process of the same Big Bang, and thus could become connected again at some time vastly distant in the future. So, copies from levels 1 and 2 have the same ontological status of actual existence (i.e. actuality, see Section 3.1.4) as any other object in the observable universe, including even your next-door neighbor.

Some scientists do not subscribe to theories of a multiverse (e.g. Hossenfelder 2018). The main argument of these critics is that, as other universes are non-observable, they are beyond real science – but this argument is obviously circular. It is, of course, difficult to prove that the universe is infinite, but to prove that it is finite is impossible, so MI cannot be disproved. Interestingly, for MI, it is not necessary that “everything possible exists” or even that the universe is of infinite size; it is only necessary that the universe is very large.

Another possible objection to the big world is the idea that only “me-now” actually exists – similar to the “moving spotlight theory” of now (Deasy 2015), “actual now” (Bitbol 1994), and “ontological privilege” of now (Frischhut and Skiles 2013) – and everything unobservable doesn’t exist. But even this will not kill the theory of multiverse immortality, as in that case, consciousness becomes an ontological necessity that helps to create the now-moment and thus can’t be turned off.

3.1.2 The finite size of human minds

Not only does the universe need to be huge, but human minds need to be finite in size for multiverse immortality to exist. As the human brain consists of a finite number of atoms (around 5x10²⁶), it seems to be finite. Tegmark shows that quantum effects do not prevent the number of states from being finite, as any quantum system in the finite space could be in only a finite number of internal states (see Bocchieri and Loinger 1957; Tegmark 2009). Moreover, the data comprising personal conscious memory has been estimated to be around 2.5 GB (Carrigan 2006), meaning that only 10^{10^10} different human minds are possible. Since most human minds will have immeasurably small differences, the actual number is even smaller.

If one looks at the observer-moment’s size, that is, the current size of an individual human being’s experience, it is dominated by the visual field, which may be roughly estimated by the size of the signal that the eye sends to the brain. It uses one million nerves in the fibers of the optic nerves, each probably presenting one pixel. By that measure, the actual size of an observer-moment can be estimated as around 1 MB, and given the presence of much non-significant peripheral noise, it is probably even smaller. Thus, there are 10^1000000 separate visual observer-moments, most of which are indistinguishable noise.

Surely, the most important part of an observer-moment is not what a person sees, but what she feels and thinks about it, but these parts are probably less complex and thus require less storage than the visual field. For example, assuming that the size of the verbal observer-moment is one sentence, and such a sentence can’t have more than 20 words, most of which are simple and frequent (and thus selected from just 1000 of the most common words) it could be concluded that there are 10⁶⁰ possible sentences, less than the number of particles in the visual universe. By these measures, the size of the human mind is, indeed, finite.

3.1.3 Sufficient diversity of the universe

An infinite universe and a finite size for human minds are not enough to prove MI. The universe must be diverse enough for any possible mind’s states to appear, because more than just repetition of events is needed: an escape from even the worst possible situations is required. Imagine that a spacecraft is falling into the Sun. At first glance, it seems that there is no chance for the pilot to survive. However, in a sufficiently diverse universe, an alien spacecraft could rescue her, or a rogue black hole moving at near-light speed could remove the Sun – or, most likely, the scenario will turn out to be just a dream.

3.1.4 “Actuality” of the existence of very remote copies

One important condition is that the whole big universe must actually exist (Menzel 2018). In short, actuality is the idea that some remote thing exists in the same way that I exist now. In a sense, actuality is “actual existence,” which implies that there is no “second-rate” form of existence. The difference becomes clear if one looks at the modal status of events in the past. Depending on the theory of time adopted, one would say that past events are either actual (in a timeless universe), or not-actual, i.e. they did exist but do not exist now, so they are more than just possible events, but less than currently extant events.

There is an open question in philosophical ontology regarding whether non-causally connected regions of space can be claimed to actually exist. However, in our case, in some theories, they are connected, as in MWI and theories of an eternal universe; or they were connected; or they will be connected. For the validity of MI, an observer’s remote copies must actually exist, or they should at least become actual in the future: if they are not actual, they do not exist. There are three solutions to the actuality problem:

1. Modal realism, that is, everything possible exists.

2. Actuality is somehow connected with the “now” moment and is “irradiated” by it.

3. “Relative actuality,” wherein actuality appears only if two objects are causally connected. In this case, unobservable regions of the universe are not actual.

In the case of QI, actuality is provided by the fact that the next observer-moment exists in the future and is causally connected with me-now. But if one starts to think about copies arising from other Big Bangs, it is easy to ask the following question. If they are so remote, and so disconnected from our universe, how could they enable a person’s immortality? This question is an intuitive expression of doubts regarding the actuality of remote copies. Intuitively, it seems that the more potential there is for the causal connection between copies, the better it is for the likelihood that MI is true, but it is not clear how well-grounded this intuition might be. There is even a point of view that if all moments of time actually exist, there should be no fear of death, as each moment will continue to exist (Deng 2015).

3.2 Condition 2: Appropriate theory of personal identity

3.2.1 The identity problem

In order for MI to work, a person should treat the continued existence of a copy of herself as a sufficient condition of her own continued existence. But can she legitimately make such an assumption? This problem is known as the “identity problem,” and its main question may be summed up as “Is information identity of minds enough for personal identity?”

Unfortunately, the correct theory of personal identity remains unknown. Although the issue initially appears simple, philosophical investigation of personal identity has notoriously turned out to be difficult, and attempts to describe the problem and the current approaches will quickly produce controversies and spill off-topic. In short, the basis of human identity is not known; for a start, the nature of consciousness and qualia are not known (Chalmers 1996), and thus the nature of the human mind and of personal identity cannot be determined.

3.2.2 The paradox of “Teleportation to Mars” and its similarity to multiverse immortality

In the Mars teleportation paradox (Parfit 1984), a person is scanned, the resulting information is sent to Mars and the person is recreated there, and the original is instantly destroyed on Earth. There seems to be no clear answer to the question of whether or not the original person has survived the process. This paradox is similar to MI, with just one difference: with MI, no data are actually sent to a remote celestial body, as the copy is already there. If a person agrees to Mars teleportation, she also should agree that the ongoing existence of remote copies, with no prospect of a future time when no such copies exist, implies some form of immortality. However, there is a caveat in the case of MI, as the number of surviving copies is constantly declining (as discussed in Section 5.1) even if it never reaches zero.

The thought experiment devised by Parfit is not a factual problem – within the thought experiment, all possible facts are known and there is nothing remaining that could be measured – but a decision-theoretical problem: a person must make a decision regarding whether or not to use the teleportation system. This decision depends on the goal system of the person and the way in which she treats her personal identity. If she must go to Mars, to, say, save her children, she should use the transportation system. However, if it is just a recreational trip, the risk of losing something important about one’s own existence is too high to make it worthwhile.

3.2.3 “Copy-friendly” and “unique-soul” approaches to the problem of the observer identity

There are three main views on the nature of personal identity:

1. Copy-friendly view: Postulates that informational identity is enough for personal identity, and any exact copy of me is me.

2. “Privileged original” point of view: Postulates the existence of some unique substrate of identity that cannot be measured from outside but which clearly distinguishes the original from the copies. The typical candidate for this substrate is either a “soul,” or a causal continuity of the human consciousness between subsequent observer-moments.

3. Open individualism: Denies the existence of the “identity” at all and postulates that all sentient beings are the same at their core.

Obviously, if some form of “soul” exists, QI will not work, as death is not real non-existence. Similarly, open individualism kills the idea of a separate, unique human, so the existence of any other mind is enough for some form of immortality to exist. Thus, only two main theories about personal identity are relevant: it is either information-only or based on causal continuity.

Causal continuity as the nature of human identity is a rather popular view, but it faces some difficult problems (Wiley and Koene 2016). For example, if a person experiences narcosis and his brain activity almost stops, should that be regarded as the death of personality? And what about the abrupt end of a dream? Causal continuity also doesn’t mean exclusivity of the next state of consciousness, as two new states could follow smoothly from the “parent” state. If QI is true, this is exactly what happens within it: minds smoothly branch into two (or more) minds with every new moment in time.

3.2.4 The merger of observer-identity and memory-identity

Identity could also be presented as two types of identity: identity as a chain of memories (which is a copy-friendly view, as any exact copy will have the same chain of memories), and identity as a chain of connected observer-moments (which is more dependent on the nature of consciousness). Moreover, the two types of identity can be separated, as demonstrated in a thought experiment by Parfit (1984), where the memories of one person are transplanted to another. These two types of identity could result in two types of QI: one as an amnestic observer, and one involving my memories in some other observer. The interaction between these two types of immortality is complex, but it may be assumed that they will eventually merge: the amnestic observer will regain her memories in some timeline, and thus it eventually will be just one type of immortality.

We, humans, experience such a merge of observer-identity and memory-identity every morning when we become awake after bizarre dreams and go through a process of remembering who we are. The same logic is applicable to the QI situation of very long and debilitating illness: there are timelines where I will regain full memory of who I am, and, in some sense, I will jump over periods of minimal or bizarre consciousness.

3.3 Personal identity theories’ connection with various types of multiverse immortality

Various combinations of personal identity theories and big world theories produce various answers about the possibility of MI. For example, if causal connection of minds is required for identity and MWI is true, then MI is a viable theory of immortality. Also, MI is a viable theory if only informational identity is required and only a cosmological inflation-based big world is true.

The relationships between the particular big-world theories and particular identity theories are presented in Table 2. This table shows how MI depends on both variables (both kinds of theories). “Yes” means that MI will work – it is a viable theory of immortality – while “No” means that it will not work. Both variables are currently unknown. Simply speaking, MI will not work if the actual world is small or if personal identity is, in a relevant sense, fragile.

Table 2. The relation between immortality, multiverse theories and personal identity theories

Big world theory Þ Personal identity theory ß	Many-worlds interpretation of quantum mechanics	Big world (cosmological inflation)	Only the visible universe actually exists
“I am only information”: copy-friendly view of personal identity	Yes	Yes	No
Causal continuity of consciousness is required for identity	Yes	No	No
Open individualism	Yes	Yes	Yes

3.4 A rough estimation of the probability that at least some form of MI is true

Looking at Table 2, it follows that in only two-thirds of the cases do the combination of personal identity theory and big world theory point to the validity of MI. Certainly, the numerical estimates are arbitrary, but they indicate that the uncertainty is very large. It is not easy to put an actual number to subjective credence in the truth or viability MI. There are serious arguments against any form of MI based on the “measure decline argument,” but a counterargument will be presented in Section 5.

This all means that a rational subject cannot be sure of either the truth or falsity of MI. Assume it should be assigned some median credence P in the theory, e.g. P = 0.5. This is not a zero result, because the consequences of MI being true or false are asymmetric. For example, a 0.5 chance of winning 1 million USD is not a zero result. As will be shown later, if MI is true, it implies a very bad outcome by default, which could turn into a very good one via relatively simple interventions. MI also causes some actions, including suicide, to have extremely negative utility.

4. Possible negative effects of multiverse immortality

A naïve view of MI is that it is some surprisingly good thing. However, there is no free lunch for immortality, and it will be shown in this section that natural MI could have negative outcomes for humanity. As will be demonstrated in Section 6, however, MI may be optimized to increase the probability of positive outcomes.

4.1 The idea of MI is an informational hazard

It seems that some people are motivated by their ethical positions to object to MI. The logic is that MI might lead an unstable person to commit suicide,⁹ so it should be claimed that QS is false. Quantum-suicide theory can be rejected if MI itself is false. However, the genie is out of the bottle; thus, it would be more socially beneficial at this stage to explain that QI has nothing to do with “suicide” – and that “quantum suicide” was an inappropriate, or even irresponsible, name, one that might lead an unstable person to think that suicide will somehow make him or her immortal. If one or another variant of MI is true, any attempt at suicide will result in failure as well as injury, and will only increase suffering; this should be explained to compensate for the potential damage of the original idea of QS.

Similarly, the idea of the existence of the soul might result in a much stronger temptation toward suicide, as it at least promises another, better world, but I have never heard that the idea was hidden for fear of resulting in suicide attempts. Instead, religions try to prevent suicide (even though suicide is logical by some of their premises) by adding additional rules against it. At this stage, it appears that MI itself does not promote suicide, and if it is correctly understood it does not entail that suicide is a good option to stop suffering. In reality, personal instability may be the main source of suicidal ideation.

If one really wants to test MI, there is no need to perform an experiment with QS. Anyone wishing to perform such an experiment would do better to wait until the age of 110. Moreover, the mere fact that the life on Earth has survived for so long in a dangerous universe – one full of gamma-ray bursts and large asteroids – for billions of years may be a case of MI, and perhaps could be interpreted as evidence for the idea.

4.2 Impossibility of death may be bad

Multiverse immortality means that death is impossible. It does not mean that any given person will definitely have a linearly infinite lifespan, as timer resets and memory loss are possible. But it means that euthanasia is impossible, and one cannot choose death, no matter how much one might desire it. It follows that there is no escape from suffering and no way to go to “another” world. If MI is true, euthanasia seems much more dangerous to a person who already suffers, because it will perpetually fail and these failures will only increase her suffering. The risk of being buried alive also becomes great if MI is true, as it is one of the most obvious forms of strange survival whose objective probability is very small, but which could present a significant share of all the ways of survival in circumstances that make it otherwise unlikely.

4.3 Long-term inescapable suffering is possible

If death is impossible, someone could be locked into a very bad situation where she cannot die, but also cannot become healthy again. It is unlikely that such an improbable state of mind will exist for too long a period – such as a period of millennia – as, when the probability of survival becomes very small, strange survival scenarios will dominate (called “low measure marginalization” by Almond (2010), 20–21). One such scenario might be aliens arriving with a cure for the illness, but more likely the suffering person will find herself in a simulation or resurrected by superintelligence in our world, perhaps following the use of cryonics.

István Aranyosi has summarized the problem as follows, referring to a previous discussion by David Lewis (2004): “David Lewis’s point that there is a terrifying corollary to the argument, namely, that we should expect to live forever in a crippled, more and more damaged state, that barely sustains life. This is the prospect of eternal quantum torment” (Aranyosi 2012, 249). If MI is true, and there is no high-tech escape on the horizon, everyone will experience his own personal hell.

Aranyosi suggests a comforting corollary, based on the idea that the suffering that is seemingly entailed by MI requires “consciousness, not life as such” (Aranyosi 2012, 252). It follows that I will not experience survival via MI if the damage to my brain is very high, and so I must find myself in a situation where I did not endure the damage to my brain that is produced by whatever is the cause of a person’s death. This means, according to Aranyosi, that being in the nearest vicinity of death is less probable than being in just “the vicinity of that vicinity” (2012, 253): the difference is akin to the difference between constant agony and short-term health improvement. However, it is well known that very chronic states of health exist that do not affect consciousness: e.g., cancer, whole-body paralysis, depression, and locked-in syndrome. I might find myself in a situation where I did not die, or even lose consciousness (perhaps for some reason that would normally appear a far-fetched possibility), but I continue to suffer pain or distress.

Fortunately, these bad outcomes become less probable for people living in the twenty-first century, as developments in medical technology increase the number of possible futures in which any particular disease can be cured or at least ameliorated, or where a person will be put in cryostasis, or wake up in the next level of a nested simulation. Aranyosi identifies several other reasons why eternal suffering is less probable than Lewis conjectured:

1. Early escape from a bad situation: “According to my line of thought, you should rather expect to always luckily avoid life-threatening events in infinitely many such crossing attempts, by not being hit (too hard) by a car to begin with. That is so because according to my argument the branching of the world, relevant from the subjective perspective, takes place earlier than it does according to Lewis. According to him it takes place just before the moment of death, according to my reasoning it takes place just before the moment of losing consciousness.” (Aranyosi 2012, 255)

2. Limits of suffering. “The more damage your brain suffers, the less you are able to suffer.” (2012, 257)

3. Inability to remember suffering. “[E]mergence from coma or the vegetative state is followed by amnesia, and in the minimal conscious state nothing more in terms of memory than recalling one’s name has been shown to be present. [...] Hence, what we should expect in the long run [...] is not an eternal life of suffering, but rather one extremely brief moment of possibly painful self-awareness – call it the ‘Momentary Life’ scenario.” (2012, 257–58)

4.4 Bad infinities and bad circles

Multiverse immortality may cause one to be locked into a very stable but improbable world – much like the scenario in the Black Mirror episode entitled “White Christmas” (aired December 16, 2014), in which a character is locked into a simulation of a room for a subjective 30 million years.

Another bad option is a circular chain of observer-moments. Multiverse immortality does not require that the “next” moment will be in the actual future, especially in the timeless universe, where all moments are equally actual. Thus, there is the possibility of a “Groundhog Day” scenario (analogous to the plot of the movie Groundhog Day, directed by Harold Ramis, Columbia Pictures, 1993). The circle could be very short, like several seconds, in which a dying consciousness repeatedly returns to the same state as several seconds ago, and as it doesn’t have any future moments it resets to the last similar moment. Surely, this could happen in only a very narrow state of consciousness, where the internal clock and memory are damaged.

4.5 Marginalization of measure, strange worlds, and infinite torture

Because of the “marginalization of measure” some very improbable and extremely bad worlds could receive a higher subjective probability. For example, a world in which future Artificial Intelligence (AI) decided to torture human beings eternally has a priori low probability, but it could be one of the most probable ways to survive almost eternally in human form.¹⁰ This is one of the types of s-risks connected with superintelligence (Sotala and Gloor 2017). In summary, MI subjectively increases the s-risks connected with AI.

4.6 Dangers of mistakenly ignoring MI and of MI-euphoria

If MI is true these several extremely bad outcomes could be real possibilities for any observer. That is why trying to dismiss MI as a weird probabilistic trick may have an almost infinite negative cost. People who strongly emotionally believe in MI may choose more risky actions, such as not fastening seat belts in a car. But the same argument is even more applicable to religious people who believe in fate. Fatalism is associated with a higher level of accidents (Şimşekoğlu et al. 2013), and why the highest world level is in Iran, a country of particularly devout people. However, the properties of MI could be used to replace bad outcomes with good outcomes for people who are currently living.

5. MI as a decision theory problem

5.1. MI and expected utility

One of the main objections to MI is the “measure decline” problem, that is, the decline of the number of copies of a given person in the multiverse. It may sound exotic, but can be presented in the form of utility expectations. In a personal communication, V. Kosoy suggested that the idea of QI should not affect our choices from the point of view of decision theory if expected utilities are correctly calculated.

Imagine a thought experiment in which QS is combined with a lottery. Bob is trying to earn money via a QS experiment (don’t do it, as most likely you will end up without money and seriously injured or dead). He asks his friend Alice to buy a lottery ticket, and he takes a sleeping pill. If the ticket is not a winner, Alice kills Bob while he is asleep. Thus, Bob will wake up only in the worlds in which he won the lottery (and Alice didn’t kill him and run away with the winning ticket).

However, the question “Did Bob actually win anything in the game?” depends on how the calculation of expected utility is performed. For example, if Bob plays a normal lottery with a probability of 0.1 of winning 1000 USD, then the expected utility of the game is 100 USD. According to the expected utility objection, this expected utility doesn’t change regardless of whether the person assumes the truth of MWI. If Bob doesn’t assume MWI is true, he has a probability of 0.1 of winning 1000 USD, i.e. 100 USD of expected utility. If Bob assumes that MWI is true, Bob should expect that, of 10 of his copies, 1 will win 1000 USD and 9 will win nothing, so, given that Bob is randomly distributed among his copies, Bob again has 100 USD of expected utility.

However, in the case of QS the situation is different, as Bob can’t be distributed between non-existent copies. In other words, if it is assumed that Bob is randomly distributed between his actually extant copies at moment t+1, the QS game becomes a winning game (as only one copy exists); however, looking at the “worlds” without Bob, the game becomes unattractive. Again, the question otherwise known as the problem of the validity of QI arises: should a decline in the number of one’s copies be regarded as death?

This thought experiment could be elaborated depending on the nature of one’s preference system. For example, imagine a mother needs 1000 USD to pay for a cure for her child. In this case, it is obvious that if she plays a QS lottery, and wins 1000 USD in 1/10 of the worlds, she leaves her child without the cure (and a mother) in 9/10 of the worlds, and this is not what she wants. Such values could be called “world-caring.” Most of our evolutionary evolved values are world-caring, as evolution favors those who have descendants in the largest share of all possible worlds.

However, there is another type of values, which doesn’t depend on the number of worlds, but instead about the existence of at least one world with some property. Consider a person who cares only about what he might feel. In that case, he could ignore worlds where he doesn’t feel anything because he doesn’t exist in them.

These two types of preferences, and corresponding solutions of the expected utility from QS, correspond to the two most accepted decision theories: causal decision theory (which cares about worlds) and evidential decision theory (which cares about experiences) (as explored by many, e.g. Soares and Levinstein 2017). Evidential decision theory seems to favor QI, as it recommends actions based only on existing experiences, and in QS a person could only experience not being killed.

However, both of these theories are imperfect: they do not account for the behavior of other agents who use the same theory, and, as a result, they recommend that agents should defect against each other in prisoner’s dilemma-type situations. For example, even if the QS lottery is a good strategy for one agent, it would be a complete disaster if everyone constantly employed it as a strategy because the world would soon be empty (and of course, money would lose its value).

To compensate for the shortcomings of existing theories, Wei Dai invented Updateless Decision Theory (UDT) (Wei Dai 2009); similar theories have also been put forward by others. The formulation of UDT is: “UDT specifies that the optimal agent is the one with the best algorithm – the best mapping from observations to actions – across a probability distribution of all world-histories” (LessWrong Wiki 2018; Armstrong 2017). This means that, if such a theory is implemented, almost all agents will typically win. UDT argues against a QS lottery, since if everybody plays such a lottery everybody will eventually lose; however, it argues for cryonics.

While many human goals are oriented to the external world, there is one important exception. Many people have an extremely negative preference for non-existence, also known as the fear of death. MI claims that there is always some form of survival – perhaps not a desirable form – but survival only in some share of all worlds, which is called “measure” because in quantum cases (as well as infinite-world cases) we cannot count worlds numerically but still need a way to distinguish between more abundant worlds and less abundant. The measure could be understood as “amount of existence” or the thickness of the Everett multiverse branch, but in normal cases, if the “measure” is measured, it will be just a Born’s rule’s probability. In the multiverse, there is a difference between having a 1 percent chance of survival and surviving with a measure of 1 percent, but this difference typically disappears in the expected utility calculations. The difference may be equal to the difference between winning 1000 USD with 0.01 probability and having 10 USD. Both events have the same expected utility, but could have different personal meanings depending on details of the preferences.

If someone has a preference for existence, MI offers a big utility gain. Moreover, if everybody were freed of the paralyzing fear of death, it might have a global positive outcome. But normal MI is bad, as shown in the previous section, so normal MI, if widely accepted, will have a negative impact on the wellbeing of people who are currently alive. However, in the case of three alternatives, MI changes the calculations of expected utility.

5.2 Merging timelines compensate the decline of measure

As discussed in the previous subsection, one of the main arguments against QI is that a person’s “measure” (or share of all worlds) declines while branching continues. However, as the person’s mental state becomes simpler when she is closer to death, she is de facto merged with “other-she” who also has a simpler mind now, but who in the past was different from the observer.

For example, imagine a thought experiment where there is an observer Alice1 with memories (M₁, M₂… M_n) and another person, Alice2, with memories (N₁, M₂…M_n); they have a different first memory. Maybe Alice1’s first cup was green and Alice2’s was yellow. If, because of the onset of Alzheimer’s, they both forget the color of their first cup, they are now the same person with memories (M₂…M_n), which basically means that Alice1’s “measure” doubled! In the case of the complexity of observer-moments, the result will be the same: the closer to death, the simpler the person’s observer-moment, and the more people she will merge with. Pereira (2017) suggested essentially the same argument as counter-evidence of the existence of very complex minds, calling it the Super-Strong Self-Sampling Assumption.

This simplification of the observer could compensate for the loss of measure because of MI. In our example, after the measure of Alices doubles, one of them could die, and the measure will again be reduced to 1. Losing 1 bit of complexity produces a doubling of the measure, so the simplification process could generate dramatic jumps in measure. For example, forgetting just 1 kilobit of personal information is equal to a 10³⁰⁰ jump of measure – enough to run the QS experiment with a 0.5 probability of death 1000 times.

If this logic about an increase in measure is assumed to be true, one could spend an evening hitting one’s head with a stone and thus losing more and more memories, and obtaining a higher and higher share of the universe. This is obviously absurd behavior for a human being, but could be a failure mode for an AI that uses the utility equation with the measure multiplier to calculate the expected utility of future states. In other words, an attempt to exclude QI by multiplying one’s gains in measure changes may pave the way to even more absurd conclusions.

But this seems to work only in the case of big world immortality, where copies are not causally connected. Whether the timelines merge in the case of the multiverse interpretation of quantum mechanics is not clear. One view is that, in quantum mechanics, a single event may have multiple histories (Feynman, Hibbs, and Styer 2010). In that case, merging seems to be possible.

Almond (2010) has suggested another argument against QI: that the decline of the number of observers means the decline of the probability of being one of them. This works in the same way as in the multiverse Sleeping Beauty thought experiment (in which Sleeping Beauty wakes 1 or 2 times, depending of the toss of a coin, either on Monday, or on Monday and Tuesday – the quantum version of the experiment was described by Peter J. Lewis (2007) and by Sean Carroll (2014)). She is less likely to be on Tuesday, as there is only one copy of her on Tuesday, but two copies on Monday. However, in the case of QI, the person always knows her time position (as t+1 in QI formalism, or Tuesday in the Sleeping Beauty case) and there is no “dissolving” of the share of observers, at least until the observer starts to forget her time position because of brain damage.

5.3. Is MI only a gambler’s fallacy?

One of the main questions raised by researchers of QI is the following: can repeated survivals in the quantum suicide experiment serve as evidence that MWI is true? Tegmark (2009) thinks that it is so, but others have suggested that such survival will be something akin to the “gambler’s fallacy.” That is, even if a person has survived a few rounds of QS, it is not evidence of any subsequent survival or of a very large size of the universe. Mallah presents an example of such thinking:

Suppose there are 10 billion people, and 200 of them decide to try QS, so about 100 of those survive. The effective probability of a person being any one of those QS survivors is about 100 in 10 billion. This is true in either the single-world or MWI case, so seeing that you are a QS survivor does not provide evidence either for or against the MWI. (Mallah 2009–2011, 5)

However, this depends on the total number of people in the world. In Mallah’s example, it is not surprising (even for an outside viewer) if around 8 rounds (≈ log₂200) of the QS lottery have survivors. However, there is only a 1 in 4096 chance in the classical world for survivors after 20 rounds, and thus their existence could be taken as evidence that the actual size of the world is much larger, i.e. it could serve as evidence for the existence of some form of the multiverse. A non-violent form of such an experiment would be survival of an observer until around 140 years old, as for centenarians median life expectancy is around 1 year, and the longest-lived person ever recorded lived only to 122.

6. Possible practical applications of multiverse immortality

6.1 Surviving until life extension technologies

Multiverse immortality – seen from a subjective perspective – may assist in escaping death, but not injuries, and thus it can imply an extended period of aging and dying, with a corresponding increase in suffering. This is the logical implication in an “ordinary,” low-tech world. Thus, there is nothing a priori good about MI.

But MI could be useful if interpreted as a probability shift in the direction required for high-quality extended life, assuming humanity could avoid putting itself at needless risk by attempting “suicide experiments.” For example, it can be posited that a sufficiently long aging process will help humans who are alive now to survive until the appearance of powerful life-extension technologies (de Grey and Rae 2007). These technologies will produce rejuvenation and might help us to live indefinitely long lives, even without the help of MI. The additional survival time needed to reach what de Grey and Rae term “longevity escape velocity” (in which additions to life expectancy outpace individuals’ aging) may be just a few decades away, and in some cases this might mean that a person does not die at the age of 50 years, but instead survives to 90. This is a rather small shift in life expectancy, which has an a priori probability of a few percent, and may be not very surprising for the person in question.

Trying to live for as long as possible provides an additional probability shift from MI, though it also produces benefits even if MI does not exist. Thus, MI should affect decisions regarding life extension.

However, MI does imply that it is better to choose medical treatments that have only two possible outcomes – immediate death or complete remission – over treatments where the process of treatment is slow and painful. For example, if a cancer patient who believes in MI has to choose between risky surgery, which could end in either remission or death, or long chemotherapy, for him it is rational to choose the surgery option, as he will observe only outcomes in which he survives. If he chose long slow treatment, he could end up in the hell-like eternity of a very damaged state.

6.2 Multiverse immortality significantly increases the chances of the success of cryonics

Multiverse immortality significantly increases the chances of cryonics succeeding at life extension. (“Cryonics” here should be regarded as a placeholder for any radical life extension or resurrection technology. Note that there is nothing especially “quantum” in cryonic technology, and that nothing in the following discussion falls within the category of quantum woo.) If MI is true, the largest share of timelines where I survive until 2100 include cryopreservation, as has previously been mentioned by Randall (2004). For example, if cryopreservation’s success chances are 0.1 percent, and my natural probability of living until the year 2100 is 1 in a million (excluding the effects of the new life extension technologies described above), I have 1000 times higher chance to survive to 2100 if I make use of cryonics. As MI entails that some instance of me will survive to 2100, it is implied that my chances of cryopreservation success grow to 50 percent (which is our estimation that MI is possible), or 500 times. In other words, no matter how small the chance of cryonics extending life may be, MI increases them up to the level of its own probability of success.

This has decision-level consequences: if, initially, you think that cryonics is not worth trying, then now, after learning about MI, you only have to sign up for cryopreservation, and MI “will do the rest.” However, if you want to be sure that your friends will also survive, you will still have to invest in the global quality and probability of the success of cryotechnologies. Signing up for cryopreservation replaces the default outcome of the “bad immortality” of infinitely long aging with a good outcome of resurrection. Signing up for cryonics is also good from the UDT point of view, as it means that other people who have similar lines of thought to your own will also sign up. If more people sign up, cryocompanies will have more money for research in improving the technology and lowering its price.

6.3 The impossibility of euthanasia and the need for cryothanasia

Euthanasia assumes that the voluntary death of a terminally ill patient will have two practical results: cessation of personal suffering, and alleviation of the burden on the patient’s relatives. The first seems to be the most important reason for euthanasia, but if MI is true, in her subjective timeline the patient will experience the failure of the procedure, which most likely means that her suffering will continue and become even worse.¹¹ Also, her hope of stopping her suffering will be ruined, and she will witness the shock of her relatives. Even if our credence in MI is only 0.5, this implies a very high probability of significantly negative outcomes.

However, if one chooses a combination of euthanasia and cryopreservation, called cryothanasia (Istvan 2014; Minerva and Sandberg 2017), the most probable line of survival will be regaining consciousness in the future when a cure for the illness has been developed. Surprisingly, this is not a popular idea.

6.4 Multiverse immortality increases the chances of the success of digital immortality, and of the acausal trade between the multiverse’s branches

Similar logic to that which favors cryopreservation in case of MI is also applicable to digital immortality, i.e. the idea that humanity will be reconstructed, based on information traces, by powerful future AI (Bell and Gray 2000; Turchin 2018b). In the face of MI, digital immortality becomes one of the most probable outcomes out of all possible ways of survival. Digital immortality could be an even more likely outcome than successful use of cryonics, as many people could be reconstructed from their information traces even if they didn’t sign up for cryonic preservation. The idea of the resurrection of the dead as a “common task” comes from the Russian cosmists, and first of all Nikolai Fedorov (see Young 2012), who hoped that all people who lived in the past would be eventually resurrected – and this surely will happen in some timelines!

However, there is a problem of information loss and resulting non-perfect resurrections. One possible solution is to replace lost pieces of information with random information (Almond 2006). In some branches of MWI these random data will be the same as my data, so an effect similar to MI will be used to reconstruct exactly me. However, what should be done with the copies that are not exactly similar? In fact, this is not a big problem, as these not-similar minds will be exact resurrections of other minds from different universes, and these universes, in turn, will resurrect me; this could be called cross-resurrection. As a result, the total measure of all resurrections will be the same and as high as if I were to be resurrected without the use of random noise.¹²

6.5 “Universal problem solver” as an example of bad implementation of multiverse immortality

Imagine a bomb, connected to a computer, that will kill me only if a certain condition is not met. In that case, I will survive in the worlds in which the condition occurs. This system is an example of a “universal problem solver”; another specific case is the QS lottery discussed above. This is a bad application of MI, as the bomb might not work, or might work ineffectively, leaving me injured but not dead; after a few attempts, such outcomes will dominate. But the main reason why this is a bad application of MI is that, if it becomes sufficiently widespread, I (along with everybody else) will soon find myself in an empty world, where everybody has killed themselves for some reason. Obviously, this would be catastrophic for my world, far outweighing any personal gain.

Almond (2008) has suggested the possibility of “civilization-level QS,” in which a whole civilization plays Russian roulette, hoping to win a needed outcome and to escape the problem of survival of only a part of its members. But such a civilization would not escape from the curse of low-measure marginalization, as it could end up in a simulation run by an adverse supercivilization. This consideration is based on the simulation argument by Bostrom (2003), which suggests that a significant share of all civilizations are past simulations run by future supercivilizations, and that different supercivilizations might have different goals for running essentially the same simulation (for example, some of them might be interested in performing non-ethical experiments, and this could be called “adverse simulation”).¹³

6.6 Collective survival in a global catastrophe

There are several ways that MI could affect the subjective probability of human extinction risks:

1. Survival of closely connected groups of people. There are several hypothetical situations in which the death of a person has highly reliable causal connections with the death of a group of people. For example, the collapse of a submerged submarine will probably kill everybody on board. In such cases, personal survival will mean that the submarine’s collapse does not happen, and it will appear that MI enhances the survival of the ship. I have previously explored nuclear submarines as possible survival refuges in the case of a global catastrophe (Turchin and Green 2017), and this effect could help increase their survivability. The same is true for a spaceship. If one sits near the potential target of a nuclear strike, it could lessen the observed probability of the nuclear war, so this approach could be used as “protection” against other global risks.

2. Observational selection effects in probability estimation of the past catastrophes. Some have suggested that the fact that humanity has survived without nuclear war may be explained by MI (Kaufman 2013). However, it is unlikely that World War Three will result in guaranteed human extinction; there will most likely be some survivors, and so this explanation seems flawed. Others have even suggested that CERN’s collider could end the world via some disaster stemming from an experiment, and that humanity currently survives (by luck) only in timelines in which the collider experiences some technical difficulties (see, for example, the views of Sandberg (2008), who offers some nice Bayesian calculations, and Yudkowsky (2008)).

3. Lone wolf survival. Even if a global catastrophe (such as a pandemic or an asteroid impact) occurs, MI entails that I could be the only survivor, as I can’t be killed from my observational point of view, although any other human being can be. Such an outcome would not technically be human extinction, but it is unlikely that I would be able to restart the civilization alone. However, I could be saved by aliens, as in Robert Charles Wilson’s 1998 short story “Divided by Infinity,” which perfectly illustrates low-measure marginalization.

4. Civilizational survival. In an entry on his Facebook page (posted December 12, 2018), the existential risks researcher Phil Torres asked whether it was certain that there must always be at least one timeline in which the entirety of human civilization survives all existential risks and ultimately colonizes space to the extent of its expanding light cone. Assuming that this is an implication of MI, such timelines will dominate the number of timelines with only one survivor. This could be regarded as a Plan D for coping with global risks, after Plan A (prevention), Plan B (survival in refuges (Turchin 2018a)), and Plan C (leaving traces of humanity (Turchin and Denkenberger 2018)).

6.7 Multiverse immortality in the age of superintelligence: will I become AI?

As mentioned above, if very advanced and powerful Artificial Intelligence appears at some point in the future, it may be able to reconstruct me based on my digital traces. MI increases the subjective probability of observation of the worlds in which AI will be interested in such reconstruction. I hope that most AIs that will practice reconstruction for the purpose of digital immortality will be benevolent and will not cause infinite suffering to the resurrected people (compare Max Daniel’s (2017) discussion of AI-related risks to humanity).

When looking at longer timelines, MI implies that the observer will exist for billions and even trillions of years. The most likely way this could happen is if the observer ultimately transforms into AI or merges with a future superintelligent (and conscious) AI.

If future AI uses MI to reach some of its goals via a form of QS lottery, it will disappear from our world, which might be good from the viewpoint of human beings. If the AI is an unfriendly “paperclip maximizer” that wants to kill all humans for their atoms (or any other reason), we could suggest some form of deal (Turchin 2017) in which AI kills all humanity instantly with 0.99 probability, and completely preserves us, or even plays the role of benevolent AI, with 0.01 probability. In that case, the AI receives 0.99 of its expected utility of killing humans (such as their atoms), but humanity enjoys collective quantum immortality (Almond 2008) and gains complete survival. As a result, the values of both entities will be satisfied.

Conclusion

In this article, one of the weird probabilistic arguments connected with our place in the universe, i.e. so-called quantum (or multiverse) immortality, was explored. Multiverse immortality has some probability of being true; though its truth is not certain, its probability is large enough for us to be wary of its bad consequences, or at least to use it as a possible multiplier to boost the chances of success of some already-existing processes, such as cryonic preservation and storage. The effects of MI on different important practices such as cryonics and euthanasia are summed up in Table 3.

Given the significant uncertainty regarding the truth of MI – and the fact that, even if MI is true, it is more likely than not to contribute to bad outcomes – it can be regarded only as a Plan D for achieving personal immortality. In this scenario, Plan A is life extension until the development of beneficial Artificial Intelligence capable of fighting aging, Plan B employs cryonics, and Plan C is digital immortality (Turchin 2015). From a practical point of view, MI is best viewed as an additive that increases the chances of success of other life extension technologies.

Table 3. The outcome matrix for multiverse immortality and significant life choices

	Normal aging	Suicide	Euthanasia	Life extension with the goal to survive until very advanced AI	Cryonics	Cryothanasia	Digital immortality	Merge with AI
MI is true	Risk of eternal suffering	Very bad (injury)	Very bad	Very good	Very good	Very good	Very good	Very good
MI is false	Neutral	Bad	Good	Neutral	Neutral	Good	Neutral	Neutral

Notes

1. However, some do find QI and related theories of immortality plausible (e.g. Loew 2017).

2. Thus, “s” stands for “suffering.”

3. Use of terms: “multiverse immortality” is the technically correct term. It is an umbrella term for two separate subtypes: “big world immortality” and “quantum immortality.” But as quantum immortality is the most accepted term, it is used throughout this paper wherever the difference between MI and QI is not material to the discussion.

4. The dust theory is best known from Greg Egan’s short story “Dust” (first published in 1992) and his 1994 novel Permutation City.

5. A good popular introduction can be found in an io9 article on quantum suicide, written by Alasdair Wilkins (2012).

6. For examples, see a Reddit discussion (Reddit c.2018), initiated by the user “rainboughost.” Participants offer numerous recollections of experiences that might potentially have been fatal.

7. Note that here “endless” does not mean “infinite,” as circular timelines are possible and actual infinity is impossible.

8. This topic is obviously controversial. For more discussion, see Friederich 2018.

9. As it seems has already happened with Everett’s daughter, Elizabeth, judging by a suicide note in which she expressed the hope – obviously impossible from the viewpoint of QI thinking – to “end up in the correct parallel universe to meet up w[ith] Daddy” (Byrne 2010, 352).

10. As in Harlan Ellison’s classic science fiction story “I Have No Mouth, and I Must Scream” (first published 1967, in the March issue of If: Worlds of Science Fiction).

11. This assumes he will have the traumatic experience of something akin to regaining consciousness in a morgue, and will feel pain again without the amelioration of painkillers, plus enduring whatever damage might have resulted from the method used in the euthanasia attempt.

12. Elsewhere (Turchin 2018c), I discuss this resurrection approach in more detail.

13. It is unlikely that civilization-level QS provides a solution for the Fermi paradox, because it is unlikely that all civilizations will choose this path, as it is clearly very risky; thus, it fails the “non-exclusivity” principle for any valid Fermi paradox solution (Brin 1983).

References

Almond, P. 2006. Many-worlds assisted mind uploading: A thought experiment.
https://web.archive.org/web/20110513092111/http://www.paul-almond.com/ManyWorldsAssistedMindUploading.htm (accessed December 22, 2018).

Almond P. 2008. Civilization-level quantum suicide.
https://web.archive.org/web/20120310105846/http://www.paul-almond.com/CivilizationLevelQuantumSuicide.htm (accessed December 22, 2018).

Almond P. 2010. Repeated quantum suicide would not suggest that MWI is correct – even to the person doing it.
https://web.archive.org/web/20120310205434/http://www.paul-almond.com/QuantumSuicide.pdf (accessed December 22, 2018).

Almond P. 2011a. Quantum suicide and inconsistency: Assuming you will survive quantum suicide may be simplistic.
https://web.archive.org/web/20120309233248/http://www.paul-almond.com/QuantumSuicideInconsistency.pdf (accessed December 22, 2018).

Almond P. 2011b. Repeated quantum suicide would not suggest that MWI is correct: A stronger version of the argument.
https://web.archive.org/web/20120310023143/http://www.paul-almond.com/QuantumSuicide2.pdf (accessed December 22, 2018).

Aranyosi, István. 2012. Should we fear quantum torment? Ratio 25(3): 249–59.

Armstrong, Stuart. 2017. Anthropic decision theory for self-locating beliefs. Future of Humanity Institute technical report.
https://www.fhi.ox.ac.uk/wp-content/uploads/Anthropic_Decision_Theory_Tech_Report.pdf
(accessed December 22, 2018).

Bell, Gordon, and Jim Gray. 2000. Digital immortality. Communications of the ACM 44(3): 28–31.

Bergström, Lars. 2012. Death and eternal recurrence. In The Oxford Handbook of Philosophy of Death, ed. Ben Bradley, Fred Feldman, and Jens Johannson, 167–85. Oxford and New York: Oxford University Press.

Bevers, Brett M. 2011. Can many-worlds survive a quantum doomsday?
http://philsci-archive.pitt.edu/8661/1/Quantum_Doomsday.pdf (accessed December 22, 2018).

Bitbol, Michel. 1994. IS NOW A MOMENT IN TIME? A discussion of McTaggart’s argument against the reality of time from a transcendental idealist standpoint. (Orig. pub. as “Now and time.”)
http://philsci-archive.pitt.edu/11560/1/Now_time_N.pdf (accessed December 22, 2018).

Bocchieri, P., and A. Loinger. 1957. Quantum recurrence theorem. Physical Review 107: 337.

Bostrom, N. 1999. The Doomsday argument is alive and kicking. Mind 108: 539–50.

Bostrom, N. 2002. Self-locating belief in big worlds: Cosmology’s missing link to observation. Journal of Philosophy 99: 607–23.

Bostrom, N. 2003. Are we living in a computer simulation? Philosophical Quarterly 53: 243–55.

Bradley, Darren. 2009. Multiple universes and observation selection effects. American Philosophical Quarterly 46: 61–72.

Braunstein, Samuel L., and Arun K. Pati. 2007. Quantum information cannot be completely hidden in correlations: Implications for the black-hole information paradox. Physical Review Letters 98: 080502-1–082502-4.

Brin, Glen David. 1983. The “great silence”: The controversy concerning extraterrestrial intelligent life. Quarterly Journal of the Royal Astronomical Society 24: 283–309.

Brown, Geoffrey. 1984. The cosmological theory of Empedocles. Apeiron 18: 97–101.

Byrne, Peter. 2010. The many worlds of Hugh Everett III: Multiple universes, mutual assured destruction, and the meltdown of a nuclear family. Oxford and New York: Oxford University Press.

Carrigan Jr., Richard A. 2006. Do potential SETI signals need to be decontaminated? Acta Astronautica 58: 112–17.

Carroll, Sean. 2014. Quantum Sleeping Beauty and the multiverse. July 28.
http://www.preposterousuniverse.com/blog/2014/07/28/quantum-sleeping-beauty-and-the-multiverse/
(accessed December 22, 2018).

Chalmers, David J. 1996. The conscious mind: In search of a fundamental theory. Oxford and New York: Oxford University Press.

Ćirković, Milan M. 2006. Is quantum suicide painless? On an apparent violation of the principal principle. Foundations of Science 11: 287–96.

Copi, Irving, and M. Cohen. 1990. Introduction to logic. New York: Macmillan.

Daniel, Max. 2017. S-risks: Why they are the worst existential risks, and how to prevent them. Foundational Research Institute.
https://foundational-research.org/s-risks-talk-eag-boston-2017/ (accessed December 22, 2018).

de Grey, Aubrey, and Michael Rae. 2007. Ending aging: The rejuvenation breakthroughs that could reverse human aging in our lifetime. New York: St. Martin’s Press.

Deasy, Daniel. 2015. The moving spotlight theory. Philosophical Studies 172: 2073–2089.

Deng, Natalja. 2015. On whether B-theoretic atheists should fear death. Philosophia 43: 1011–1021.

Egan, Greg. 2009. Dust Theory FAQ.
http://www.gregegan.net/PERMUTATION/FAQ/FAQ.html (accessed December 22, 2018).

Eliade, Mircea. 2005. The myth of the eternal return. Trans. Willard R. Trask. 2nd paperback ed. Princeton, NJ: Princeton University Press. (Orig. pub. 1949.)

Feynman, Richard P., Albert R. Hibbs, and Daniel F. Styer. 2010. Quantum mechanics and path integrals. Emended ed. New York: McGraw-Hill.

Friederich, Simon. 2018. Fine-tuning. Stanford Encyclopedia of Philosophy (Winter 2018 ed.).
https://plato.stanford.edu/archives/win2018/entries/fine-tuning/> (accessed December 22, 2018).

Frischhut, Akiko M., and Alexander Skiles. 2013. Time, modality, and the unbearable lightness of being. Thought: A Journal of Philosophy 2: 264–73.

Higgo, James. 1998. Does the “many-worlds” interpretation of quantum mechanics imply immortality?
https://web.archive.org/web/20050203192203/http://higgo.com:80/quantum/qti.htm
(accessed December 22, 2018).

Hossenfelder, Sabine. 2018. Scientific theory and the multiverse madness. National Public Radio.
https://www.npr.org/sections/13.7/2018/01/22/579666359/scientific-theory-and-the-multiverse-madness (accessed December 22, 2018).

Istvan, Zoltan. 2014. Should cryonics, cryothanasia, and transhumanism be part of the euthanasia debate? Huffington Post. June 23 (updated August 21).
https://www.huffingtonpost.com/zoltan-istvan/should-cryonics-cryocide-_b_5518684.html
(accessed December 22, 2018).

Jones, Jonathan A. 2017. Technological resurrection: A thought experiment. [No publication details provided.]

Kaufman, Jeff. 2013. Is our continued existence evidence that mutually assured destruction worked? LessWrong. June 19.
https://www.lesswrong.com/posts/9miMdHERJFjQDp5uq/is-our-continued-existence-evidence-that-mutually-assured (accessed December 22, 2018).

Kaufmann, Walter A. 2013. Nietzsche: Philosopher, psychologist, antichrist. Princeton, NJ, and Oxford: Princeton University Press. (Orig. pub. 1950.)

LessWrong Wiki. 2018. Updateless decision theory.
https://wiki.lesswrong.com/wiki/Updateless_decision_theory (accessed December 22, 2018).

Lewis, David. 2004. How many lives has Schrödinger’s cat? Australasian Journal of Philosophy 82: 3–22.

Lewis, Peter J. 2007. Quantum Sleeping Beauty. Analysis 67: 59–65.

Loew, Christian. 2017. Boltzmannian immortality. Erkenntnis 82: 761–76.

Mallah, Jacques. 2009–2011. Many-worlds interpretations can not imply “quantum immortality.” arXiv:0902.0187 [quant-ph].
https://arxiv.org/ftp/arxiv/papers/0902/0902.0187.pdf (accessed December 22, 2018).

Marchal, Bruno. 1991. Mechanism and personal identity. In Proceedings of WOCFAI, 91: 335–45.

Menzel, Christopher. 2018. Actualism. Stanford Encyclopedia of Philosophy (Summer 2018 ed.).
https://plato.stanford.edu/archives/sum2018/entries/actualism/ (accessed December 22, 2018).

Minerva, Francesca, and Anders Sandberg. 2017. Euthanasia and cryothanasia. Bioethics 31: 526–33.

Moravec, Hans. 1988. Mind children: The future of robot and human intelligence. Cambridge, MA: Harvard University Press.

Mülle, Markus P. 2018. Law without law: From observer states to physics via algorithmic information theory. arXiv:1712.01826v2 [quant-ph].
http://arxiv.org/abs/1712.01826 (accessed December 22, 2018).

Page, Don N. 2007. Susskind’s challenge to the Hartle-Hawking no-boundary proposal and possible resolutions. Journal of Cosmology and Astroparticle Physics 01(January)004: 1–20.

Parfit, Derek. 1984. Reasons and persons. Oxford and New York: Oxford University Press.

Pereira, Toby. 2017. An anthropic argument against the future existence of superintelligent artificial intelligence. arXiv:1705.03078v1 [cs.AI].
https://arxiv.org/ftp/arxiv/papers/1705/1705.03078.pdf (accessed December 22, 2018).

Randall, Allan F. 2004. Quantum miracles and immortality. Quantum 5(8).
Available online http://www.allanrandall.ca/tv2004.pdf (accessed December 22, 2018).

Reddit. c.2018. Quantum immortality. Is the glitch the fact that some people remember being reset? (Discussion of quantum immortality initiated by user “rainboughost.”)
https://www.reddit.com/r/Glitch_in_the_Matrix/comments/6j7pi5/quantum_immortality_is_the_glitch_the_fact_that/ (accessed December 22, 2018).

Sandberg, Anders. 2008. Bayes, Moravec and the LHC: Quantum suicide, subjective probability and conspiracies. Andart blog. September 22.
http://www.aleph.se/andart/archives/2008/09/bayes_moravec_and_the_lhc_quantum_suicide_subjective_probability_and_conspiracies.html (accessed December 22, 2018).

Shikhovtsev, Eugene B. 2003. Biographical sketch of Hugh Everett, III.
http://space.mit.edu/home/tegmark/everett/everett.html#contents (accessed December 22, 2018).

Şimşekoğlu, Özlem, Trond Nordfjærn, Mohsen Fallah Zavareh, Amin Mohamadi Hezaveh, Amir Reza Mamdoohi, and Torbjørn Rundmo. 2013. Risk perceptions, fatalism and driver behaviors in Turkey and Iran. Safety Science 59(November): 187–92.

Smolin, Lee. 1992. Did the universe evolve? Classical and Quantum Gravity 9: 173–91.

Soares, Nate, and Benjamin A. Levinstein. 2017. Cheating death in Damascus. Technical report. Machine Intelligence Research Institute.
https://intelligence.org/files/DeathInDamascus.pdf (accessed December 22, 2018).

Sotala, Kaj, and Lukas Gloor. 2017. Superintelligence as a cause or cure for risks of astronomical suffering. Informatica 41: 389–40.

Squires, Euan J. 1994. The mystery of the quantum world. 2nd ed. New York and Oxford: Taylor & Francis.

Steinhardt, Paul J., and Neil Turok. 2002. Cosmic evolution in a cyclic universe. Physical Review D 65: 126003-1–126003-20.

Tegmark, M. 1998. The interpretation of quantum mechanics: Many worlds or many words? Fortschritte Der Physik 46: 855–62.

Tegmark, M. 2009. The multiverse hierarchy. arXiv:0905.1283 [physics.pop-ph].
https://arxiv.org/pdf/0905.1283v1.pdf (accessed December 22, 2018). (Orig. pub. 2007.)

Turchin, Alexey. 2015. Immortality roadmap. LessWrong. July 29.
http://lesswrong.com/lw/mjl/immortality_roadmap/ (accessed December 22, 2018).

Turchin, Alexey. 2017. Messaging future AI. Manuscript.
https://goo.gl/YArqki (accessed December 22, 2018).

Turchin, Alexey. 2018a. Approaches to the prevention of global catastrophic risks. The Human Prospect 7(2): 52–66.

Turchin, Alexey. 2018b. Digital immortality: Theory and protocol for indirect mind uploading. Manuscript available at PhilPapers. https://philpapers.org/rec/TURDIT (accessed December 22, 2018).

Turchin, Alexey. 2018c. Resurrection of the dead via multiverse-wide acausual cooperation. LessWrong. September 3.
https://www.lesswrong.com/posts/BJfb2hqtdnaRijAfz/resurrection-of-the-dead-via-multiverse-wide-acausual
(accessed December 22, 2018).

Turchin, Alexey, and Maxim Chernyakov. 2018. Classification of approaches to technological resurrection. Manuscript available at PhilPapers.
https://philpapers.org/archive/TURCOA-3.pdf (accessed December 22, 2018).

Turchin, Alexey, and David Denkenberger. 2018. Surviving global risks through the preservation of humanity’s data on the Moon. Acta Astronautica 146: 161–70.

Turchin, Alexey, and Brian Patrick Green. 2017. Aquatic refuges for surviving a global catastrophe. Futures 89: 26–37.

Wei Dai (2009). Towards a new decision theory. LessWrong. August 13.
https://www.lesswrong.com/posts/de3xjFaACCAk6imzv/towards-a-new-decision-theory
(accessed December 22, 2018).

Wiley, K.B., and R.A. Koene. 2016. The fallacy of favoring gradual replacement mind uploading over scan-and-copy. Journal of Consciousness Studies 23: 212–35.

Wilkins, Alasdair. 2012. Quantum suicide: How to prove the multiverse exists, in the most violent way possible. Io9. March 8.
https://io9.gizmodo.com/5891740/quantum-suicide-how-to-prove-the-multiverse-exists-in-the-most-violent-way-possible
(accessed December 22, 2018).

Young, George M. 2012. The Russian cosmists: The esoteric futurism of Nikolai Fedorov and his followers. Oxford and New York: Oxford University Press.

Yudkowsky, Eliezer. 2008. How many LHC failures is too many? LessWrong. September 21.
https://www.lesswrong.com/posts/jE3npTEBtHnZBuAcg/how-many-lhc-failures-is-too-many
(accessed December 22, 2018).