Design of a Primitive Nanofactory

 Journal of Evolution and Technology  -  Vol. 13 - October 2003  -    PDF Version
http://jetpress.org/volume13/Nanofactory.htm

Chris Phoenix
Director of Research, Center for Responsible Nanotechnology http://CRNano.org
 

Abstract:

Molecular manufacturing requires more than mechanochemistry.  A single nanoscale fabricator cannot build macro-scale products.  This paper describes the mechanisms, structures, and processes of a prototypical macro-scale, programmable nanofactory composed of many small fabricators.  Power requirements, control of mechanochemistry, reliability in the face of radiation damage, convergent assembly processes and joint mechanisms, and product design are discussed in detail, establishing that the design should be capable of duplicating itself.  Nanofactory parameters are derived from plausible fabricator parameters.  The pre-design of a nanofactory and many products appears to be within today's capabilities.  Bootstrapping issues are discussed briefly, indicating that nanofactory development might occur quite soon after fabricator development.  Given an assembler, a nanofactory appears feasible and worthwhile, and should be accounted for in assembler policy discussions.

Contents:
1. Introduction
2. Background
    2.1. Mechanochemistry
    2.2. Mechanochemical fabricator designs
    2.3. Parts assembly, scaling, and product integration
    2.4. Nanofactory overview
3. Components and Innovations
    3.1. A Thermodynamically Efficient Stepping Drive
        Figure 1: Pin Drive
    3.2. Joining Product Blocks
        3.2.1. The Expanding Ridge Joint
           Figure 2: Expanding Ridge Joint
        3.2.2. Functional joints
4. Nanofactory Architecture
    4.1. Mechanochemical functionality
        Figure 3: Workstation Grids
    4.2. The reliable basic production module
        Figure 4: Production Module
    4.3. Gathering stages
        Figure 5: Convergent Assembly Fractal Stages
    4.4. Casing and final assembly stage
        Figure 6: Nanofactory Layout
    4.5. Issues in bootstrapping
    4.6. Improving the design
5. Product design
    5.1. Levels of design
        5.1.1. Nanoparts
        5.1.2. Nanomachines
        5.1.3. Nanoblocks
        5.1.4. Patterns and Regions
        5.1.5. Folds
        5.1.6. Networks
    5.2. Simulation and testing
        5.2.1. Design and simulation
        5.2.2. Testing and debugging a nanofactory-built product
6. Control of the nanofactory
    6.1. Nanocomputer architecture and requirements
    6.2. Placing the nanoblocks
    6.3. Specifying the nanoblocks
7. Product Performance
    7.1. Strength, stiffness, and shape
    7.2. Appearance
    7.3. Complexity
    7.4. Design
    7.5. Powering the product
    7.6. Computation
8. Nanofactory calculations
    8.1. File size and data distribution
    8.2. Fabricator control, energy, and cooling
    8.3. Physical arrangement and mass
    8.4. Product cycle, duplication, and bootstrapping time
    8.5. Radiation and failure
    8.6. Cost and difficulty of manufacture
9. Conclusion and discussion
Appendix A. Calculations in software
Appendix B. Projections from the Merkle assembler
    B.1. Mechanochemical baseline
    B.2. Chemistry, electronics, and mechanics
    B.3. Mechanochemical error rate
References

1. Introduction

This paper builds on previous proposals to describe an architecture for combining large numbers of programmable mechanochemical fabricators into a manufacturing system, or nanofactory, capable of producing a wide range of human-scale products.  The proposed system is described in sufficient detail to allow estimation of nanofactory mass, volume, power requirements, reliability, fabrication time, and product capability and cost, as simple functions of the properties of the mechanochemical fabricator component.  Bootstrapping a human-scale system from a sub-micron system is also discussed.  Discussion of product design issues and nanofactory manufacturing capability demonstrates that the nanofactory should be able to efficiently fabricate duplicates of itself as well as larger versions.  This proposal differs from previous proposals in that, with the exception of mechanochemical component fabrication, design of the nanofactory should be within the reach of present-day engineering; physical structures and functional requirements are described in sufficient detail that remaining problems should be within the capability of current engineering practice to solve.  In particular, the design considers all transport and manipulation requirements for raw materials and product components, as well as control, power, and cooling issues.

This exploration can provide a basis for estimating the practical value and difficulty of developing a nanofactory.  As noted in (Merkle, 1999), even a primitive sub-micron mechanochemical fabricator may produce valuable products.  The question at hand is whether, once such a device is developed, it is feasible and worthwhile to adapt such devices into a nanofactory.  Since no complete designs, or even complete parameter sets, exist for a mechanochemical fabricator, this question cannot be answered fully at this time.  However, the results of the present paper can be applied to a wide range of hypothetical fabricator parameters.  As fabricator designs are proposed in increasing detail, these results will become increasingly useful in predicting the capabilities of a nanofactory based on such designs.  Issues of product design and manufacture are examined in order to establish that the nanofactory is capable of fabricating duplicates and larger versions of itself.  The time required to bootstrap a human-scale factory from a nano-scale fabricator cannot be estimated with any certainty, since bootstrapping will require time for debugging and redesign as well as for fabrication of larger versions.  However, the minimum time required for fabrication can be estimated, and the design developed here is simple enough that debugging and redesign may be fairly simple and rapid.

The paper is arranged in several sections.  Section 2 surveys previous work toward manufacturing systems relying on mechanochemistry and producing human-scale products.  Section 3 describes two innovations required for efficient operation of the nanofactory architecture.  Section 4 describes the nanofactory architecture, including a highly reliable production module incorporating several thousand mechanochemical fabricators and a scalable convergent assembly and transport architecture for integrating large numbers of production modules.  Section 5 covers issues of product design to establish that the nanofactory is designable and buildable by itself.  Section 6 discusses computer control of the nanofactory.  Section 7 covers product performance.  Section 8 provides calculations relating nanofactory performance and characteristics to fabricator performance and characteristics.  Section 9 summarizes the paper.  Appendix A is a computer program that implements repetitive calculations for probability, size of components, and pressure in cooling channels.  Appendix B is a brief discussion of the suitability of a proposed fabricator design (Merkle, 1999) for the nanofactory architecture.

2. Background

2.1. Mechanochemistry

In order to focus on nanofactory architecture, the present work does not consider mechanochemical operations in detail.  Instead, the design assumes the existence of a small programmable mechanochemical fabricator.  To simplify architectural considerations, the fabricator is assumed to be self-contained: it must be capable within a small volume of performing all mechanical motions necessary to fabricate parts from feedstock and assemble them into small devices of complexity comparable to itself.
 

2.2. Mechanochemical fabricator designs

The robot arm requires several different mechanical components, including small gears, triply-threaded toroidal worm drives, and several types of cylindrical sliding interfaces.  Each of these components may require significant atom-level design.  In addition, the robot arm requires a control system involving rotational motion on several drive rods.  Nanometer-scale clutches have not been designed in detail.  In order to provide results relevant to early fabricator and nanofactory development, this paper does not assume that devices of such complexity can be built.   Hall's parts synthesizer requires separate assembly robots to deliver chemicals, and the power/control mechanism is not specified.

Systems relying on many biologically-based feedstock molecules require separate synthesis and assembly areas, which may have quite different environmental requirements.  In addition, they may require nontrivial transport mechanisms to prevent premature reaction of the feedstock molecules.  Finally, such systems do not appear to permit the fabrication of diamondoid structures.

The molecular mill is an attractive concept for several reasons.  It does not require explicit control of each mechanochemical operation, thus greatly increasing efficiency over the other three proposals.  Operations can also be quite fast, since merely moving a belt a short distance is sufficient to accomplish a mechanochemical operation.  However, each reactive encounter mechanism, or station, in a molecular mill performs only one mechanochemical operation.  Although each station is efficient, in the sense of processing a mass equal to its own in a short time and with little energy wasted, a large number of stations would be required to fabricate all the parts needed to build a nanofactory, let alone the desired range of products.  This number has not been quantified.  Additional design would be required to explain how a number of stations performing different mechanochemical operations and using different parts can produce all the required parts for self-replication given that only one chemical operation is performed at each station.  Although this does not contradict the possibility of a self-replicating set of mills, it indicates that the set may be large and difficult to design.  In addition, the set may grow unpredictably when required to produce additional parts for the non-fabricator portions of the nanofactory, and may need significant modification if the design of a part must be changed.  Accordingly, a mill solution is not used in this paper.  However, it should be noted that a combination of a mill making small blocks and a double tripod capable of both joining blocks seamlessly (Drexler, 1992, sec. 9.7.3) and performing detailed mechanochemistry may be fast, flexible, and relatively easy to design, and would be preferable to the simple robotic manipulator implicitly assumed for this baseline design.

The current design effort is based loosely on a double-tripod "assembler" discussed by Merkle (1999).  Merkle's assembler is self-contained, simple to control, and approximately the right size for a basic factory or product building block.  Every effort has been made to avoid depending on any specific property of Merkle's design.  However, the claimed feasibility of this design serves as inspiration for the present effort to integrate designs with comparable functionality into a monolithic nanofactory.
 

2.3. Parts assembly, scaling, and product integration

Large-scale cooperative designs are not well understood today, and directing them may be expected to be difficult.  Hall (1993) describes a "utility fog" composed of many small identical robots.  Such a system would be relatively simple to manufacture, requiring no large-scale assembly.  Hall suggests that the fog could use any of several fairly simple algorithms to simulate solid objects.  However, he also does not consider how to power the product/object, and the control algorithms are not worked out in detail.  Also, his fog is quite weak for its mass, at least compared to a more strongly fastened diamondoid product.

The purpose of the nanofactory is to build strong, functionally rich, monolithic, human-scale products that are easy to design and use.  Several innovations described in this paper allow a nanofactory design to be presented in detail for the first time.  The nanofactory itself is intended to be in the set of possible products.  The paper focuses on early development and on demonstrably feasible designs, so does not include some obvious but currently speculative techniques for improving performance.  The design is deliberately simple, especially in minimizing the amount of mechanochemical design needed in addition to the preexisting fabricator.  The major design effort focuses on mechanical and digital design, physical layout, and fault tolerance.

Mechanical design methodology has achieved great competence in the transformation of mechanical motion and force.  Many devices have been developed to accomplish this, such as cams and followers, rack and pinion drives, planetary and differential gears, and pantographs.  Drexler (1992, chap. 10) demonstrated that many of these devices can be translated directly to nanometer scale.  However, many of Drexler's designs use a specialized arrangement of surface atoms, and sometimes of internal atoms.  Such devices would require individual chemical design.  To avoid the unknown but potentially large effort involved in developing new chemical synthesis for new mechanical structures, the present design does not generally assume the use of mechanical features smaller than ~1 nm.  Such a design is referred to as "bulk diamond", meaning that simply specifying a suitable volumetric design to be filled with diamond lattice is sufficient to specify a part with the required mechanical function.

Although a wide range of sensing and feedback technologies have been developed at the macro scale, some of them do not work at the nanometer scale (e.g. optics and electromagnets; see Drexler, 1992, sec. 2.4), and others may require excessive volume or complexity.  In general, this design effort avoids sensing in favor of predictability and reliability.  Digital logic is useful for performing repetitive functions, doing precise calculations, and selecting among alternatives using well-specified criteria.  Software systems that interact with mechanical systems may be hampered by sensor data that are not well specified.  Accordingly, this design does not make much use of feedback, or require software to deal with "fuzzy" situations.  Almost all aspects of nanofactory operation are deterministic; this mirrors the (theoretically) deterministic nature of the mechanochemical technique (Drexler, 1992, sec. 6.3).  Because the factory layout is extremely repetitive and strictly hierarchical, issues in controlling a large number of fabricators and robots can be reduced to controlling a single fabricator or robot, plus simple iteration.

As previously noted, this paper builds on work which demonstrates that a nanofactory is conceptually feasible.  The design presented here is sufficiently detailed that the feasibility of each part of it can be assessed.  However, it is sufficiently general that it can accommodate a variety of mechanochemical systems.  Where design principles are well understood, details are not supplied.  For example, the use of a gantry crane is specified in order to demonstrate the existence of robotics capable of doing the job required, and to allow approximate calculation of the mass of those components.  The drive mechanism of the gantry crane is not specified; however, given a design tolerance of 1 nm and the presumed feasibility of motors  as small as 50 nm in diameter (see Section 8.2), it is clear that such a mechanism can be designed in a wide range of sizes; at the present level of design, it is not necessary to examine work on industrial robotics.

The extreme conservatism that is appropriate for a feasibility demonstration is less appropriate for a preliminary engineering study.  For example, it is conservative to assume that each individual part will require individual design at the atomic scale.  However, it is reasonable to assume that in the case of a rod with bumps regularly spaced on it, the rod can be extended and bumps can be added or removed without requiring detailed redesign.  Thus the use of mechanical digital logic designs (Drexler, 1992, chap. 12) is assumed to require a mechanochemical design effort for only a fixed and relatively small number of parts.  Likewise, the quantitative sections of this paper choose typical or reasonable values instead of extreme or pessimistic values.
 

2.4. Nanofactory overview

The exact size of the nanoblock is unimportant.  For this design, a 200-nm cube is convenient: it is large enough to contain a simple 8086-equivalent CPU, a microwatt worth of electrostatic motors/generators, a shaft carrying 0.4 watts (Freitas, 1999, sec. 6.4.3.4), or the Merkle assembler (1999), but small enough to be fabricated quickly and to survive background radiation for a useful period of time.  As discussed in Section 6, the partitioning of the product into nanoblocks, and the use of relatively large sub-blocks at each step, allows the use of relatively simple robotics and control algorithms in the nanofactory.  As discussed in Section 5, such division also simplifies product design without imposing many practical limits on product complexity.  (W. Ware points out that a combination of tetrahedra and truncated tetrahedra is also space-filling, and that this may be more compatible with the tetrahedral diamond matrix.)

At the smallest scale, the organization of the factory changes to allow simpler distribution of feedstock, cooling, power, and control, and simpler error handling.  A production module consists of one computer and a few thousand fabricators.  It produces a few blocks, a few microns in size, by combining a few thousand nanoblocks.  These rectilinear production modules incorporate a few block assembly stages.  They are combined into the smallest factories, which are also rectilinear--and so on to any size desired.  At each stage, product blocks are delivered through the center of the smallest face, allowing compact stacking of multiple modules or stages.  The stages are stacked on either side of a gathering/assembly tube which contains simple robotics to join the incoming product blocks into larger blocks and deliver them out the end of the tube.  Two stacks of stages, plus the tube in between, constitute the next higher level stage.

The nanofactory design is highly repetitive: each input (sub-factory, or substage) to a stage is identical.  Thus only one design is required for each level, regardless of the number of substages at that level.  Since each stage joins eight blocks to form one block with twice the linear dimension, 19 sizes of stage (4 internal to the production module) are required to progress from a 200-nm nanoblock to a 10.5-cm product.  (One additional stage, a simplified gathering stage, is used to transition from production modules to gathering/assembly stages.)  Most of these stages perform identical block-joining operations.  The design of one stage may be used with minor modification for several similar stage sizes.

A nanofactory built with primitive fabricators and control systems may use a lot of power.  It will be cooled by a fluid with suspended encapsulated ice particles (Drexler, 1992, sec. 11.5).  Thus the temperature of the nanofactory will be a uniform 0 C (273 K).  This is significant for the energy used by digital logic (Section 8.2) and for aligning and joining large blocks (Section 3.2.1).

The control architecture of the nanofactory, like the physical arrangement, is strictly hierarchical.  Instructions can be distributed from central computers directly to the computers that directly control the fabricators.  All error detection and correction takes place either within a single nanocomputer or within a production module controlled by a single nanocomputer, and error reporting and compensation are not required beyond the production module.  There is no need for communication between any two computers at the same level; a simple tree architecture can be used to send all required data (Section 8.1).  Exotic or complex control algorithms, networking architectures, and operating systems are not required.

The size, mass, energy requirement, and duplication time of this nanofactory design depend heavily on the properties of the fabricator.  Sections 8.2, 8.3, and 8.4 quantify these relations.  With the assumptions made in those sections, a tabletop nanofactory (1x1x1/2 meters) might weigh 10 kg or less, produce 4 kg of diamondoid (~10.5 cm cube) in 3 hours, and require as little as fifteen hours to produce a duplicate nanofactory.
 

3. Components and Innovations

The fabricator used in the nanofactory is unspecified; the nanofactory design is sufficiently general that a wide variety of possible fabricator designs can be incorporated.  The reader may find it helpful to study Merkle's "assembler" (1999) (Appendix B) as a prototype.  The only requirements are that the fabricator must be capable of producing a variety of products of size and complexity equal to itself from soluble feedstock molecules, and that it use digital deterministic control, which implies that the mechanochemical processes must be highly reliable.  Since only a few reactions will be sufficient to make a wide variety of molecular shapes, and since error detection and correction will be difficult if not impossible in early broadcast-architecture assemblers, these requirements do not greatly reduce the generality of the present design.  (Unreliable operations can be retried multiple times even in a deterministic system; see for example Drexler, 1992, sec. 13.3.1c).
 

3.1. A Thermodynamically Efficient Stepping Drive

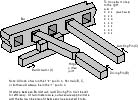
Figure 1: Pin Drive

An efficient drive with functional characteristics similar to the ratchet drive is the pin drive.  (See Figure 1.)  In this design, pins are inserted into equally spaced holes (or notches) in the moving bar to assure its position at all times.  The latching pin moves in and out but not sideways, and is used to hold the bar still.  The driving pin moves in and out, and also is moved sideways by a bar actuator over a distance equal to the spacing of the holes.  The pins are similar in structure and function to the rods in Drexler's rod logic design.  To move the bar one step, the bar actuator is moved to one end of its range, pulling the driving pin into alignment with a hole.  The driving pin is inserted.  The latching pin is withdrawn.  Then the bar actuator is moved to the other end of its range, bringing the next hole into alignment with the latching pin, which is then inserted.  Finally, the driving pin is withdrawn and then moved back to its original position.  Smaller step sizes may be obtained by additional offset pins, or by a second vernier drive, similar to the vernier ratchet drive described by Drexler (1992, sec. 16.3.2), with slightly different hole spacing and bar actuator range of motion from the main drive.  Larger step sizes may be obtained by moving the bar actuator a larger distance in each cycle.

Although the pin drive requires one more actuator than the ratchet drive--two pins and a bar actuator, instead of two ratchet pawl pullers--it has the advantage that it can move by measured steps in either direction, whereas the two-ratchet drive can only move stepwise in one direction and must retract in a single motion by lifting both ratchets.  (If both pins are lifted simultaneously, the bar can be moved without restriction by a weak return actuator, allowing the same rapid return motion as the ratchet drive.  Note that without careful design, verifying the complete return of the bar will require energy on the order of 100 kT.)  Similar redesign can be applied to any stepping drive mechanism.  As long as the position of the moving member is initially known, it can be moved stepwise, held stiffly against thermal noise at every point, and locked in place in its new position, all without irreversible state transitions.

While the pins are moving, the bar is stationary and the pins may be moved reversibly.  As the bar actuator is moved, the force encountered may vary.  Nevertheless, stiffly imposed motion will be efficient in most cases.  As long as the force profile of the motion does not vary more rapidly per distance than the stiffness of the drive mechanism, and does not vary substantially between forward and backward motion (e.g. due to an irreversible state transition), it does not matter how much force is required to move the bar at each point because the energy will be recovered when the motion is reversed.  This energy recovery requirement implies that the drive mechanism must be able to recover energy from being driven by the bar; such designs are not difficult, and include Drexler's electrostatic motor/generator (1992, sec. 11.7).  The same argument applies to other types of actuators driven by other digital control mechanisms: as long as the force profile is reversible and is less steep than the stiffness of the drive mechanism, the energy that is put into the system is recoverable.  Note that rapid motion causes the force profile to deviate from reversibility due to various energy dissipation mechanisms.  (The author thanks Eric Drexler for clarifying discussion of thermodynamic reversibility.)
 

3.2. Joining Product Blocks

At very small separations, two objects experience an attractive force called van der Waals force: simply bring them close together, and they stick.  For two flat diamond surfaces, the force is approximately 1 nanonewton per square nanometer, or 10,000 atm of pressure (Freitas, 1999, sec. 9.3.2).  This is reasonably high, although it provides only a fraction of the strength and stiffness of chemical bonds.  The van der Waals force is the simplest method of joining, it is reversible, and it should provide sufficient strength to keep even kg-scale products from falling apart under their own weight.  This type of joint is convenient and can be used for weak joining of structures that must later be separated.

A diamond surface that is not passivated with an outer layer of hydrogen will be very reactive.  Unterminated diamondoid surfaces forced together should form covalent bonds.  According to Drexler, two (110) surfaces of tetrahedral diamond or two (100) surfaces of hexagonal diamond should bond to each other on contact, forming a seamless joint (Drexler, 1992, secs. 8.6, 9.7.3, and 14.2.1).  Sinnott et al. (1997) report the results of simulations that show bond formation, though not seamless joining.  For other diamond surfaces, or in the case of too-rapid joining, a somewhat weaker joint may form with a lower bond density.  Also, it is currently unknown how much pressure would be required to initiate the process.  Crushing buckyballs to diamond requires 20 GPa, but Drexler states (personal communication, January 24, 2003) that a covalent joint should "zipper" itself if started at an edge or corner, that neon atoms should be able to escape the closing gap and would not interfere with the joining, and that argon is even better in this regard.  If the joint were comparable in structure to amorphous diamond currently made for MEMS, it would have a tensile strength of only 8 GPa (Sullivan, 2002); this is significantly less than diamond's tensile strength of 60 GPa (measured) to over 100 GPa (calculated, depending on crystal orientation) (Telling et al., 2000).  An additional problem is that radiation damage or stray molecules may cause local surface reconstruction or contamination that may hold surfaces apart and prevent a joint from forming.  This type of joint is usually not reversible, though in theory a carefully designed edge might allow predictable crack formation.  Since seamless covalent joints have not yet been demonstrated, the present nanofactory design does not use this method.
 

3.2.1. The Expanding Ridge Joint

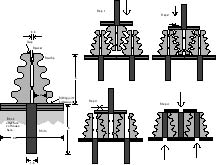
Figure 2: Expanding Ridge Joint

The triangular shape of the ridges has several advantages.  First, the area of the base of the triangles (almost the entire area of the block surface) is structurally solid.  (By contrast, a square ridge would waste at least half of the structural strength of the blocks being joined, because the block area adjacent to the tops of the ridges would not contribute to the joint.)  Second, at small scales, van der Waals forces make handling of components difficult because the components stick to any manipulator.  With triangular ridges and narrow ridge tops, the contact area of the surface is much lower, reducing the van der Waals force.  Third, a manipulator can easily be aligned with the ridges.  Small blocks can be picked up by simple contact with a V-channeled manipulator that presents sufficient surface area to form a van der Waals bond of the desired strength, and the manipulator will automatically be pulled into alignment.  A more complex mating pattern could fasten on several ridges at once.  If the ridges are placed at varying angles or spacings, a well designed manipulator/ridge interface can guarantee that a misaligned manipulator cannot form a firm grip.  Likewise, a well designed ridge/ridge interface can guarantee that misaligned blocks will not join incorrectly.

There are at least three ways of mounting the ridge so that a small attractive force between mating ridges will be sufficient to cause the ridge to spread.  The first possibility is to join the ridge to the nanoblock with dovetail joints, permitting it to slide sideways with very low friction.  A simple dovetail joint costs somewhat more than half of the possible joint strength; a stairstepped dovetail joint (which is similar to a completed ridge joint) would recover much of the strength at the cost of additional volume and complexity.  The second possibility is to use a mounting that is strong in tension but flexible in shear, such as thin columns of diamond or buckytubes.  The third possibility, for use in linear stacks of many nanoblocks, is to build a solid structure extending from the base of the ridge all the way through the block to the ridge on the opposing face.  Both ridges would move in tandem, and be locked in place when the shims were dropped on each side.  This might require a mechanism for retaining all participating shims until all joints are pressed together.

The simplest version of the expanding ridge joint requires no actuation to form the joint other than moving the faces together.  As the faces are brought together, just before the final closure, each row of scallops brushes past the inverse row on the opposing ridge.  As the interlocking ridges from each surface interpenetrate, the bulges of the scallops brush past each other, close enough to be attracted by van der Waals force.  This pulls the halves of the ridge apart.  The attraction between passing scallops when the faces nearly touch must be stronger than the intra-ridge attraction, to ensure ridge spreading during the last phase of joint insertion, as the final rows of scallops pass each other.  This is ensured by the use of small spacers to control the van der Waals force holding the intra-ridge gap closed.  (The spreading will become increasingly favorable as the faces approach, and the operation will happen slowly enough to allow equilibration, so thermal noise will not cause the joint to fail to close.)  However, the intra-ridge attraction (between halves of the same ridge) must be strong enough in the initial position to prevent premature operation due to thermal noise.  The half-ridges must require a certain energy, say 100 kT, to pull them apart far enough for the shim to be inserted; the displacement which absorbs this energy cannot be greater than the depth of the scallop.  Note that the required energy is not dependent on any spatial parameter; it is related only to temperature.  However, the attractive force is approximately proportional to surface area, so this condition can be satisfied by a sufficiently long ridge joint.  In other words, regardless of the actual inter-scallop force, an intra-ridge gap can be chosen that will allow the ridge halves to be separated; and regardless of the gap, a sufficiently long ridge will be resistant to premature separation.

Due to the complicated geometry of the scallops, exact calculation of the attractive force between mating ridge halves is beyond the scope of this paper.  An inaccurate calculation is given to permit crude estimation of minimum ridge length.  The formula for attraction between cylinders (Drexler, 1992, Fig. 3.10f) will be applied, treating each scallop as a 0.5-nm radius cylinder separated by 0.3 nm.  (This is inaccurate because it ignores the attractive contribution from the material behind the cylinders, and because the formula's derivation assumes that cylinder radius is much greater than cylinder separation.)  The inter-scallop potential energy is calculated as 61 zJ per linear nanometer of scallop contact, which corresponds to 2 nm^2 of surface between the two halves of the ridge.  To reduce the intra-ridge potential energy to 50 zJ per scallop-nm or 25 zJ per nm^2, the spacing must be at least 0.6 nm (ignoring the attractive contribution from the spacer) according to the formula in (Drexler, 1992, Fig. 3.10d) which slightly overestimates the attractive force since the ridge is not infinitely thick.

When the gap between the half-ridges is fully open, the shim (which includes a hollow to accommodate the spacer) is pulled into the gap and held there reliably by van der Waals force.  The shim will insert when the ridges have moved apart by a distance equal to the depth of the scallop undercut, in this example 1 nm.  With a 1-nm deep scallop and a 0.6 nm initial gap (thus a 1.6-nm wide shim), the difference in potential energy between 0.6 nm and 1.6 nm spacing is 21.5 zJ/nm^2.  To prevent premature insertion, the intra-ridge potential energy of attraction must differ by 100 kT (260 zJ at 0 C) between closed and open positions.  This requires 12 nm^2 of intra-ridge gap.  If the ridge is 8 nm high (with 4 scallops), then it need only be 1.5 nm long.

The joint may be stiffened by compressing the joint volume.  In this case, extra force may be used to insert the shim into the gap.  (This also allows the gap to be somewhat narrower, reducing non-structural volume.)  A simple design for an electrostatic actuator adds only one moving part.  The shim is blanketed between insulated capacitor plates, one of which is flexible.  Charging the capacitor makes the plates pull together, expelling the shim like a watermelon seed.  The electricity to power the actuator can be delivered through contact with small embedded conductors at the proper time during the convergent assembly process.  The tip of the shim can be tapered to help spread the ridge halves.  Once the shim is expelled, the capacitor plates will adhere to each other by van der Waals force, forming a reliable barrier to hold the shim in the joint even if the capacitor is discharged.

Tension on the joint will tend to expand the entire joint volume sideways.  This can be constrained by surrounding each joint (not each ridge) with a diamond collar sufficient to resist the sideways force generated by a single ridge.  The ridge joint is somewhat less stiff in tension or compression than solid diamond would be, but should be almost as strong: failure requires either significant compression of a large volume of diamond, or the simultaneous failure of many covalent bonds.  Effectively, the entire joint volume except for the depth of the scallops and the width of the shim contributes to the tensile strength, and the entire joint volume except for the shim contributes to the compressive strength.  Shear strength and stiffness depend on the orientation and attachment of the ridges, but can be made quite high perpendicular to the ridge line.  Torsional and bending strength and stiffness can also be made quite high.

The width of the shim is unrelated to the size of the ridge, being equal to the depth of the scallop's undercut plus the intra-ridge van der Waals gap.  A reasonable lower bound for component size is a ridge composed of four scallops 1 nm deep and offset by 1/2 nm horizontally and 2 nm vertically.  The height of the ridge is 8 nm, and the footprint of a half-ridge is 3.5 nm (accommodating 0.5 nm of motion to mate with the opposing half-ridge), of which 2 nm contributes structural strength.  The 1.6-nm wide shim adds an additional 0.8 nm of non-structural overhead to each half-ridge; the total joint tensile strength is approximately 47% of solid diamond.  (Shallower scallops will improve this number up to a point; scallops that are too shallow can fail by slipping past each other.)  For reliable operation the ridge must be at least 1.5 nm long.  The smallest joint consists of one half-ridge on each side, only one of which (and its shim) needs to move; the rest of the joint including the mating half-ridge can be solid diamond.  A single joint can potentially have a footprint smaller than 3x6 nm.  Larger ridges can have more scallops, with the size of each scallop (and thus of the shim) staying constant.  For example, a half-ridge 20 nm high with 10 scallops has a footprint of 6.5 nm (plus 0.8 nm for its share of the shim) of which 5 nm is structural, for 68% of diamond strength.  Covering a 200-nm block with 8-nm-high ridges on each side requires 8% of the block volume (ignoring block edges and corners).  However, in a high-strength application that requires ridge joint coverage of the full surface, the block must be nearly solid diamond anyway.

Because the strength of the joint decreases only slightly with smaller size (the decrease is a function of the minimum shim, scallop, and van der Waals gap size), small ridges are mechanically adequate for joining blocks at any scale.  Minimum ridge size is determined by the mechanochemical fabrication process.  The only limitations on block size are the precision of the block-handling machinery and the possibility of unequal expansion of the faces due to temperature differences.  With 200 nm nanoblocks, ridges built in a single block can be up to 100 nm in height, with tops 50 nm apart.  (Note that the blocks will overlap by the height of the ridge.  The change in effective block width during assembly presents issues for the assembly process that are straightforward but beyond the scope of this paper.)  An assembly tolerance of 0.05 micron is somewhat beyond today's standards; current state of the art for automated pick and place assembly for optical components appears to be around 0.5 micron (Blaze Network Products, 2003).  However, today's pick and place systems use hardware made with a manufacturing tolerance comparable to its performance.  In contrast, the dimensional precision of the nanofactory's hardware will be approximately one atomic diameter or less, regardless of scale.  At large scales, single ridges can be assembled from multiple nanoblocks, allowing ridge spacing of multiple microns; this is sufficient even for today's robotics.

Differences in fabrication processes, assembly processes, and internal structure may cause different blocks to be at different temperatures.  The resulting thermal expansion can cause a misalignment of the ridges.  The volumetric thermal expansion coefficient of diamond is 3.5x10^-6/K (Freitas, 1999, Appendix A); the linear coefficient is one-third that, or 1.2x10^-6/K.  A temperature difference of 1 K thus causes a 200 nm block to expand by a small fraction of an angstrom, while a 10.5-cm surface will expand by 126 nm.  Because diamond is an excellent conductor of heat, passive equilibration may be sufficient.  As long as the displacement is not greater than the ridge spacing, or the ridge pattern does not permit improper joining, the blocks may be pressed together slowly, allowing the temperature to equalize.  Even a rarefied internal atmosphere will also facilitate temperature equalization between nearby faces, though this process may be slow depending on block mass, and the process will be somewhat slower with argon than with neon.  Note that the nanofactory is cooled by phase transition (see Section 8.2), so the cooling fluid will have the same temperature throughout the factory, minimizing potential product temperature differences.  Active compensation might involve sensing the temperature at various points on the surfaces and applying heat to the cooler surface via embedded resistive heaters; this will only be necessary for the few large-scale joints that take place near the end of the assembly process, and the heating process can be initiated in advance to avoid delay.  Embedded mechanical (bi-material) thermostats can allow each region to reach a preset temperature without individual attention.

Because the joints require no external manipulation or assembly force, they can be used to fasten non-bonded parts that are only loosely connected to the main nanoblock.  For example, a structural beam one micron long and 50 nm wide can be constructed in five sections.  Each section will be terminated in ridge joints, and laid across a nanoblock in a position that will place the section ends next to each other during block assembly; van der Waals force will hold the section in place during block manipulation.  When the nanoblocks are assembled, the ridge joints of the beam will join at the same time as the rest of the joints, with no additional effort.  This allows the inclusion of long, thin components in product designs.  Likewise, single nanoblocks can be made in separate pieces joined by van der Waals force.  This allows a block to be pulled apart during the unfolding process, forming multiple walls with large spaces between them.  This can be useful to save mass where only thin walls are needed.  If a block is split into as many as 10 walls or 100 columns, the 20-nm width is sufficient for multiple full-sized ridge joints on each part.  This capability is assumed for interior nanofactory structure.

Joints can be formed after the product is released from the factory, as long as contaminants have been excluded from the joint space.  The factory can manufacture a larger containing balloon for product unfolding, or the joints can be protected individually by a variety of covering mechanisms.  A product can be created in a very compact form, then unfold like a pop-up book or like flat-packed cardboard boxes.  Components can be built in pieces, with lightweight pantographic trusswork to bring the ends together as the product expands; once the ends touch, the strong joint will form. A component can also be made in a "broken" state, with mating surfaces held together on one edge with a small hinge at any desired angle, and the open end protected by a bellows if necessary.  When the component is straightened, the mating surfaces will form the desired strong connection.  A weak and reversible joint can be formed by preventing the shims from entering the gaps between the ridges.  This allows blocks to be loosely connected, then disconnected, and finally reconnected tightly in the same or different configuration.  This may be useful if the unfolding process requires a structure to be produced in its final conformation, then flexed, and finally fastened rigidly.
 

3.2.2. Functional joints

Embedded wires can be run up to a flat face, and electrical contact made by tunneling.  Contact can be maintained in the case of joint strain by the use of springy interfaces.  According to measured values for a sample of HOPG (highly ordered pyrolitic graphite), (GE Advanced Ceramics, 2002) graphite is about 5000 times more conductive in-plane than cross-plane (and the in-plane value is 1/50 as good as a typical metal).  The separation of graphite planes is 0.335 nm, about 1/600 of the 200-nm nanoblock width.  This implies that a graphite-graphite tunneling surface of 8 nm^2 per nm^2 of graphite wire, spaced every 200 nm, would only double the total resistance.  To save nanoblock surface area, the tunneling surface can consist of interlocking corrugations.  Because diamond is an excellent insulator, high voltages may be used to compensate for the resistance of graphite.  Some buckytubes may be better conductors.

Control cables and control rods will be built into each nanoblock when it is manufactured, and extend only to its edges.  Tension and/or compression must be transferred between blocks.  Nanocomputer logic rods have ends ~1 nm^2 which can be butted together.  The nanocomputer design uses tensional force of 2 nN (Drexler, 1992, sec. 12.3.3.b) but this can be traded for displacement or compressive force without sacrificing reliability.  Alternatively, the joint area can be increased by a few nm^2 to allow a few nN of tensile force to be transmitted through van der Waals attraction.  Crossing between blocks may require adding extra logic gates to transform and condition the signal; this logic can all be reversible at some cost of time.  Such interfaces will not add significantly to the power requirements or design complexity of a nanocomputer.

Polyyne (carbon chains with alternating single and triple bonds) control cables can be terminated with a small diamondoid plate flush with the nanoblock surface.  When the blocks are joined, the plates will stick by van der Waals force.  Each two atoms of polyyne spans a length of 0.2569 nm and has a compliance of 0.00185 m/N (Casing an Assembler, "Control cables").  A 1-nm diamond cube contains 176 carbon atoms.  A van der Waals interface has a stiffness of >30 N/m per nm^2 (Drexler, 1992, sec. 9.7.1), or a compliance of <0.0334 m/N.  Two hundred nm of polyyne contains 1557 carbon atoms and has a compliance of 1.44 m/N, while 198 nm of polyyne interrupted by two 1-nm diamond cubes interfaced by van der Waals force contains 1893 carbon atoms and has a compliance of 1.47 m/N; the interface increases cable mass by 22% and compliance by 2% (ignoring the hydrogen termination and internal compliance of the diamond cubes) and may introduce resonances into extremely high-speed operations.  The main drawback of the interface is its strength; the tensile strength of a polyyne rod is >6 nN, but the strength of the interface is ~1 nN.  Increasing the interface area allows a stronger and stiffer joint, and for joint areas above a few square nanometers a ridge joint can be used at some cost of mass.

Power can be transmitted by means of thin rotating rods, embedded in the nanoblocks like the control cables and logic rods.  Mating convolutions on rod ends will allow the transmission of torque between ends that are simply pressed together.  If the rod is driven near maximum torque, the interface may need to be somewhat larger than the cross section of the rod.  The bursting speed of a disc decreases in proportion with its radius, while the area increases as the square of the radius; thus a 2x increase in interface area will cause a 1.4x reduction in speed.  In this simple example, power transmission is derated by 40%; however, other mechanical linkages such as a thin belt connecting offset and overlapping rods may permit full speed while delivering full torque.  (The belt can be placed around one rod during nanoblock manufacture and held open by any of a variety of methods.  The other rod can be tapered to slip inside the belt during block assembly.  Interlocking (gear-toothed) rod surfaces will also work but may require significant overlap for reliable torque transmission.)  Rods and shafts larger than a few nm can be joined by ridge joints.  Ridge joints may also serve as a means of chocking the shafts to ensure proper alignment, and then unlocking them during convergent assembly: the shims can be inserted only when the joint is fully closed, and the motion of their insertion can be used to remove a mechanical chock.  Small rods can be controlled by adjacent ridge joints, and large shafts by facial joints with internal shims.

Bearing surfaces for rotating shafts small enough to be embedded in nanoblocks can be built into each nanoblock during construction.  Variations in rod diameter will prevent the rods slipping out of the block prior to convergent assembly.  Large rods pose a special problem for convergent assembly, since they cannot be strongly and permanently fastened to a support or bearing structure.  However, for products up to 10 cm size, a tight-fitting bearing surface between a rod and a housing can provide the necessary adhesion by van der Waals force alone.  Rotational freedom can be constrained by small retractable chocks.  Graphite pads covering the matching surfaces of the blocks constituting the shaft and the blocks constituting the housing can provide a bearing surface even for slightly rough curved surfaces.  However, the boundaries between the pads will be aligned on the moving and bearing surface, and this can create a significant force.  (Twisting one of the surfaces relative to the other would break the alignment, but this will not be possible for cylindrical bearings.)  Order-of-magnitude calculations can be made by treating the boundary gaps as regions of wider spacing between the surfaces, calculating the difference in van der Waals energy between aligned and unaligned regions, and dividing that by the width of the gap to find a force.  Approximating the boundary as a trench 1 nm wide and 0.1 nm deep and the pad spacing as 0.2 nm, and applying the formula from (Drexler, 1992, Fig. 3.10d), indicates an energy difference of 81 zJ per nm^2 in favor of the aligned state, or an average force of 81 pN per linear nm of trench.  One mm^2 of flat sliding surface will contain 5x10^9 nm of trench crossing the direction of motion, creating a force of ~0.4 N.  However, the stiffness of 1 mm^2 of graphite bearing surface is ~3x10^13 N/m, so for many macroscopic applications, bearings may be made small enough that the "roughness" is not a significant problem.  A cylindrical bearing surface cuts across two nanoblock planes and only a fraction of the area contributes to stiffness; these factors increase the number of trenches (and thus the "roughness" force) for a given bearing stiffness by approximately a factor of 4.

Pipes are simply voids in the diamond nanoblocks that are butted together when the blocks are assembled.  A flat, uncompressed interface between nitrogen-terminated diamond (111) surfaces is adequate to exclude helium (Drexler, 1992, sec. 11.4.2a).  If this type of interface proves inadequate in practice (perhaps due to joint flexure, or unavailability of nitrogen termination chemistry), a conical extension of the pipe wall wrapped in one or more layers of graphite to provide a compressive seal and extending into a conical depression in the other block should suffice.  Pipes too large to be contained inside a nanoblock can be sealed by diamond or graphite curtain walls, placed along each seam, to separate the interior of the pipe from the mechanical joint area.  If the nanofactory is filled with inert gas, pipes will also be filled with the gas when they are manufactured.  If this is a problem, one possible solution is to place a collapsed graphite tube inside the pipe, terminating the tube ends at the nanoblock faces with a diamond mating collar thin enough to be flexible.  When the blocks are assembled, the collars join.  When first used, the graphite tube will expand and conform to the walls of the pipe while displaced gas can be vented through small channels.
 

4. Nanofactory Architecture

The nanofactory is built hierarchically, using only a few scalable designs.  At the lowest level, a few thousand fabricators are arranged in a planar grid.  Their products are picked up and assembled into increasingly large blocks by a series of increasingly large robotic manipulators.  This plus a control computer constitutes a basic, reliable production module.  The production modules are stacked three-dimensionally into gathering stages, which assemble blocks and pass them to higher-level gathering stages.  Finally, the entire factory is enclosed in a suitable casing, with a mechanism to output product without contaminating the workspace.

In Merkle's convergent assembly architecture (1999) it is suggested that each convergent assembly stage has four inputs, each supplying two blocks to make one output block.  However, this means that each input to the preceding stage must supply four blocks to make those two, and so on.  This is feasible if blocks can be manufactured extremely quickly, or (as in Merkle's design) fed through a relatively small number of ports efficiently.  The current design, using large nanoblocks requiring minutes or hours to fabricate, uses only one block from each fabricator per product cycle.  This implies that each stage will receive all its blocks in parallel.  In general, then, each stage must have either eight (non-redundant) or nine or ten (redundant) inputs.  (The first gathering stage has only four inputs, to compensate for the eighteen inputs of the final stage in the production module; see below.)

4.1. Mechanochemical functionality

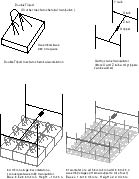
Figure 3: Workstation Grids

Fabricators will be fastened together edgewise to form the planar array, which divides the coolant volume from the working volume.  Cooling fluid with dissolved feedstock circulates past one side; the products (nanoblocks) are fabricated and released on the opposite side, which is open to the nanofactory's clean working volume.  A square of nine fabricators (one redundant) forms a stage.  Product blocks are picked up by a three degree of freedom gantry crane manipulator and assembled into a 0.4-micron block.  Likewise, a square of nine of these stages forms the next stage.  This continues through several levels; in the current design, four levels is chosen for suitable redundancy and convenient control.
 

4.2. The reliable basic production module

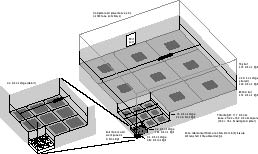
Figure 4: Production Module

The physical layout is similar in some respects to Merkle's architecture for convergent assembly (Merkle, 1999).  Substage outputs are be grouped on one wall of an assembly chamber, forming the inputs to the stage; substages are placed side by side, and stages are stacked on top of substages.  See Figure 4.  As in Merkle's design, the output from a stage is twice the width of each input; unlike Merkle's design, each input port delivers only one block per product cycle instead of two.  The design is not quite scalable, since the width of the assembly stage is three times the width of the sub-stage, while the width of the block that is produced is only two times the input block size.  The ninth substage is redundant, used in case of failure of another substage.  Four levels of redundancy are probably sufficiently redundant for a nanofactory of the size contemplated here.  Otherwise, more redundancy can be added in a fifth stage, or by extending a gathering stage; see Section 8.5 for calculations.

The module's top and bottom surface are completely covered with 9^4 = 81^2 = 6561 mechanochemical fabricators each.  To provide space for moving sub-blocks around a growing assembly, each stage is 3.1 times as high as the sub-block it receives.  Two of these assemblages are sandwiched together, sharing a single 3.2-micron assembly stage, to make one production module that produces two 3.2-micron blocks per product cycle.  The design can be compacted somewhat if multiple convergent assembly stages can be combined; such optimization is beyond the scope of this paper.  The CPUs, memory, DMA controllers, and motors are placed on the face that contains the output port, forming a single layer and extending the width by 0.2 micron.  Controlling a column of 81 fabricators requires perhaps a few billion bits per second and <100 pW (Section 8.2), which fits through an interface requiring only a few nm^2.  Only 4096 fabricators per side are used at any time; the rest are redundant, to be used in the event of radiation damage.  See Section 8.5 for further discussion of this design.  Powering the entire set of 8192 fabricators plus the computer requires 8 nW, far smaller than the 500 nW capacity of a single electrostatic motor.
 

4.3. Gathering stages

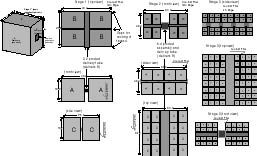
Figure 5: Convergent Assembly Fractal Stages

The factory does not require a hierarchical network of computers, since the computation is done either at the top level or at the level of individual production modules (see Section 6).  Once the blocks are fabricated, a fraction of the production module computers can be used to run the convergent assembly robotics.  If hierarchical computers are needed, the computers can be built into the tube walls.  Amplification will be needed to distribute the top-level signal to each of the production modules.  This can be implemented in each stage, and can be combined with a mechanism to send a unique, hard-coded position indicator to each production module.  By knowing which branch the signal takes at each stage, the module's computer can easily determine the position of its output in the final product.

A tabletop factory might produce a 10.5-cm product; this is 2^15 times larger in linear dimension than the 3.2 micron output of a production module, so product assembly requires 14 further assembly stages where each stage assembles 64 sub-blocks to produce eight product blocks.  See Figure 5, and Section 8.3 for dimensions.  A final stage, external to the factory, is described in the next section; it assembles eight 5.25-cm sub-blocks (per product cycle) to produce the final product.  Note that the first stage in the Figure is not an assembly stage, but serves only to gather 8 sub-blocks for delivery to the next stage, since each production module makes only two blocks per product cycle.  Each assembly stage gathers 64 sub-blocks from substages, assembles them within the assembly/delivery tube, and delivers the 8 assembled blocks to the superstage.  With the current size parameters, in some of the smaller stages, a minimum-volume arrangement leaves the tubes perhaps too short for simultaneous assembly of 8 blocks.  Four blocks may have to be assembled and passed on to the next stage, and then the other four assembled; this adds only fractionally to the total product cycle time.  The Stage 1 delivery tube is fractionally larger than the 3.2-micron product it carries.  The other assembly/delivery tubes are large enough to allow moving sub-blocks to fit past the product block under construction.
 

4.4. Casing and final assembly stage

Figure 6: Nanofactory Layout

The overall nanofactory shape is a rectangular solid.  The exterior shell consists of six flat panels enclosing the necessary volume.  Each panel provides support to anchor the interior and prevent the working volume from collapsing under atmospheric pressure.  (Cooling fluid pressure will be contained by the tension members crossing the cooling gaps, and will not put additional force on the external casing.)  This is equivalent to a 1-atm pressure difference between the inside and outside of each exterior panel, imposing a bending force.  In addition, the panels support each other, experiencing a crushing force at each edge.  The panels are hollow and pressurized.  Internal tension members, set at a slight angle, keep them rigid and flat.  Since the working volume contains the lowest pressure in the nanofactory, no pressure bracing needs to be installed inside that volume; the cables only intrude on the cooling channels.  With many small cables supporting them, interior walls can be very thin.  See Sections 8.2 and 8.3 for a discussion of structural mass and coolant and panel pressure.  Sufficiently numerous and thin cables (no thicker than the walls) cannot tear the walls; since the cables can be as thin as a buckytube, details of attachment need not be considered.

In the final gathering stage, multiple blocks (up to 8 per product cycle) are pressed together to form the final product.  The product must be delivered without allowing contaminants into the factory.  One way to do this is to produce a rectangular solid extruded through a sliding seal, as in the "replicating brick" approach of Merkle (Drexler, 1992).  This constrains product configuration, requires that all faces be smooth, and does not provide a protected environment for post-assembly unfolding.  An alternative design, permitting much greater flexibility in product shape, is to enclose the final stage in a balloon, the neck of which forms a sliding seal with the factory.  A new balloon is installed for each product, pushing the old one (with previous product) out and preventing contamination.  The mechanism of the final assembly stage must be extended for some distance outside the factory during final product assembly, but still requires only three degrees of freedom.  Once the product is assembled and optionally unfolded, the assembly mechanism is retracted and a new balloon is installed.

Most of the nanofactory mechanism is maintained at low or zero pressure to reduce drag on moving parts.  To allow balloon inflation, the final convergent assembly tube is used as an airlock, pressurizing it with pure neon or argon after all 64 sub-blocks have been delivered.   If low pressure in the factory is tolerable, the airlock need not be scavenged completely before the end of the next product cycle, and mechanical pumping will be sufficient.  If even a few atoms of noble gas cannot be tolerated in the factory or included in interior voids of the product, the airlock can be scavenged by use of a cryogenic surface; since neon and argon do not adsorb at room temperature, "bake out" is unnecessary and the airlock can be completely emptied of gas in a relatively short time.  The design of the assembly mechanism, airlock mechanism, and balloon installation is straightforward.
 

4.5. Issues in bootstrapping

Several imaging technologies may be useful.  Electron microscopes have a very fine resolution and form images rapidly, but use multi-keV electrons.  Single-wall nanotubes can be imaged in an electron microscope without apparent damage, but high-energy electrons may penetrate a single graphite layer and either do chemical damage to sensitive bonds or charge insulating surfaces, which could cause undesirable electrostatic forces that would probably interfere with operation.  Vapor deposition of metal on the outer surface of the fabricator before imaging may alleviate this problem.  Scanning probe microscopy may be useful for imaging the probes as they are aligned with the fabricator.  Non-contact AFM (atomic force microscopy) can avoid displacing the probes due to contact forces.  Optical interferometric methods may be useful for feedback on at least one dimension of alignment.  Finally, two-part fluorescent systems (e.g. absorber and fluorescer, or absorber/fluorescer and quencher), with one part attached to the fabricator and the other attached to the probe, may be useful for final alignment (Drexler, 1992, sec. 16.3.6c).  The number of probes to be attached is small--only four for the first several bootstrapping steps.

The moving-plate electrostatic actuator described in (Drexler, 1992, sec. 11.6.4) requires a plate area of only 150 nm^2 and provides 1000 zJ per actuation.  A 100 MHz cycle time requires 100 pW.  The actuator is powered by 5 volts, requiring a current of 20 pA.  This current is far lower than the 0.1 mA that has been measured in a single buckytube (Ipe Nanotube Primer, 2001), so buckytubes can be used to deliver power for initial bootstrapping stages.  A manipulation system like the Zyvex three-probe SEM manipulator (MinFeng et al, 1998) can place buckytubes with 6-nm precision on separate pads on the fabricator.  A ground connection can be made through the surface the fabricator rests on.  This can supply power for several actuators, which can control any number of internal systems if one of the actuators is used to drive a simple mechanical selector.

If the fabricator is in a dry environment, feedstock must be delivered via a closed system.  Hollow glass needles can be drawn as fine as 30 nm (Intracel LTD, 2001) which is small enough to interface directly with a single fabricator.  Two needles are needed to maintain a flow of fresh solvent past the molecular intake port; this accommodates designs that reject waste molecules as well as designs that use varying amounts of multiple chemicals during the fabrication process.  A housing over the molecular interface with two 40-nm holes partially closed by 10-nm graphite sheets should allow a leak-proof, though not strong, interface to the needle tips.  The tips can be positioned using the same kind of manipulator used to position the buckytubes, and held in place during the fabrication operation.

A single fabricator has space inside its casing to make two duplicates with separate shells.  Instead, it could fasten the two together, side by side, and combine the shells.  This would give roughly four times the internal working volume for the same area of shell, and the two fabricator stages could each produce two 200-nm blocks.  A single additional ratchet would select whether the actuation was to be delivered to one or the other fabricator, or both together.  (Either the electricity or the resulting mechanical motion could be switched.)  Most of the time, both fabricators could be working in synchrony, so the same control signals could be routed to both of them; duplication time would not be greatly increased.

Since the two fabricators are placed side by side, their products would also be adjacent.  When fabrication was finished, each double tripod would have sufficient range of motion to grab its finished product and move it into contact with the other.  A single 1 nm^2 contact area would apply 1 nN of force.  The weight of even a 10-micron cube, containing 125,000 nanoblocks, is 0.035 nN, allowing over 10 gravities of acceleration.  With small step sizes, torsion from off-center moving force can be relaxed after each step; since only a single motion of a few nm is needed, this will not significantly affect duplication time.

As the device grows, more different kinds of blocks will be required, but more electrical control channels can be added.  Blocks containing convergent assembly manipulators will be mostly empty space, so will not require much fabrication time to complete if they must be built one at a time.  An internal CPU will not be required until the stage where it is a small fraction of the overall device mass.  Once the device is sufficiently large that at least six control channels can be attached, the manufacture of the CPU and RAM can proceed in parallel with the manufacture of the fabricator blocks without affecting duplication time.

There are many suitable physical layouts for the medium-scale devices.  For example, mechanochemical modules could form plates to line the top and bottom of a wide workspace, with the plates separated by 800 nm.  Each module would make two nanoblocks, extending them vertically into the workspace until they touched the nanoblocks from the opposite side.  The resulting product would be four nanoblocks thick; each face of the nanoblocks would be either strongly fastened to its neighbor or weakly held by van der Waals forces.  When the product was completed, the tripods working in concert would pass it out one side of the factory which would open onto a balloon large enough for the product to unfold into a flat factory of twice the area.  A slightly more advanced design stacks several of these flat factories and includes a 1 DOF (degree of freedom) manipulator extending into the balloon to push together (and thus join) the product slabs after they have been extruded; this allows more complex unfolding.  The maximum workable size of this design is limited by radiation damage.  A factory of 16,000 fabricators (a suitable size for one nanocomputer to control, with the program downloaded in stages to save memory) may have a 1% chance of suffering a disabling hit to a single fabricator in a single day (see Section 8.5).
 

4.6. Improving the design

The current design is extremely wasteful of power.  It is also limited in the speed at which it can work.  The inclusion of "mills" for early-stage chemical processing (Drexler, 1992, sec. 13.3) can save orders of magnitude of power and significant time.  A mill does not require any computation to perform an operation.  Additionally, a mill can more easily recover energy from exothermic reactions, and even from the final stages of endothermic reactions.  With mills preparing small diamond cubes or hexagonal carbon chains that can be covalently bonded to each other (Drexler, 1992, sec. 8.6.5b), a hybrid mill/manipulator system could produce bulk diamond far more quickly and efficiently.  Because mills require both mechanical and chemical design, they have not been included in the current nanofactory design.

The inclusion of atoms other than carbon and hydrogen allows flexibility of design.  In particular, Kaehler brackets (1990) would allow more precise designs of surfaces and orientations.  To some extent, mechanochemistry can be developed by simulation in advance of fabricator availability.

Even without using additional chemistry, stepwise actuation can be made more efficient and faster.  Current design requires a separate operation for every step, and each operation requires computation and time.  A non-stepping mechanism might be an improvement.  For example, a set of stops could be included in the path of a sliding bar.  A chosen stop would be extended, all other stops disengaged, and a linear actuator used to move the bar rapidly until the stop is contacted.  The force profile of the actuator is problematic.  For efficiency, its force must be weak over most of the displacement, but for resistance to thermal noise, it must apply a strong force at the end of the cycle.  (A combination of a weak actuator and a slow but strong latching pin may also be efficient.)  An alternative is to use several drive mechanisms with varying step sizes, some of them large, or to design the pin drive so that in a single cycle it can move either one or several steps.

Many other mechanical and chemical improvements will be obvious.  The development of improved nanofactory models may be expected to proceed quickly, and manufacturing performance will also increase quickly.  Performance of products will increase somewhat as a result of continued research and development.  By several measures, products produced by the current nanofactory design are already within an order of magnitude of theoretical limits.  It should be noted that no part of the current design requires such levels of performance.
 

5. Product design

5.1. Levels of design

5.1.1. Nanoparts

One of the most complex components of the nanofactory will be the nanocomputers.  A nanocomputer of Drexler's design (1992, chap. 12) consists of only a few types of parts, including logic rods with varying combinations of knobs, a few kinds of springs, cams, a motor/flywheel, and a housing.   Although the computer may contain thousands of different rod configurations, all rod designs can be synthesized from knobbed and knobless segments; each additional rod thus requires only a few bits to specify knob positions.  Assembly of the parts into the nanocomputer will also be repetitive, as much of the circuitry consists of regular arrangements of rods in programmable logic arrays.  Translating from a digital logic specification to a mechanical hardware arrangement is straightforward.

Mechanical devices large enough to be specified with bulk diamond construction are also large enough that their strength and stiffness can be treated with classical approximations (Drexler, 1992, chap. 9).  Although other effects such as electron tunneling between conductors may be significant, a purely mechanical design can usually ignore them.  The main difference between nanoscale mechanical design and macroscale design will be surface effects including van der Waals force.

Nanopart designs may be parameterized.  For example, instead of a different part specification for each length of buckytube, a single specification can be given with a start, a finish, and a middle component that can be repeated as desired.  The nanocomputer logic rods are another parameterized part.  It should be possible to specify complex volumes of diamond in terms of geometric description.  As discussed in Section 6, the choice of whether to parameterize a part or to specify its variants separately will depend on a tradeoff between processing power and memory space.
 

5.1.2. Nanomachines

The level of nanomachines is not strictly necessary; parts could be assembled directly into nanoblocks.  However, the use of this level of specification causes no loss of capability and is convenient since human designers think in terms of machines.  A nanomachine specification, then, includes some sequence of nanoparts and sub-components together with a sequence of assembly operations that assemble the sub-components.  Sub-components may be considered as nanomachines in their own right; this saves space in the product description file, as one sequence of parts and operations can be included in several machines by reference.
 

5.1.3. Nanoblocks

In the current nanofactory design, a nanoblock is a 200-nm cube.  If a typical diamondoid part occupies a 10 nanometer cube (which has space for ~176,000 diamond-lattice atoms) then 8,000 parts can fit inside each nanoblock.  For comparison, a typical 4-cylinder automobile engine has ~450 parts (Whitney et al., 1998).  As in the nanocomputer design (Section 6.1), where the CPU occupies one cube and memory is placed in adjacent cubes, designs can often be broken along convenient planes and placed in adjacent cubes, communicating through pipes, small control rods, electrical wires, or larger mechanical interfaces.

The simplest nanoblock is inert--solid structural diamond, with full structural ridge joint coverage at one or more faces.  Another class of nanoblock is filled with digital mechanical logic; several nanoblock designs are needed to implement a nanocomputer.  A third class of nanoblock could be filled with actuators; a nanoblock full of electrostatic motors could convert a microwatt, and the same block would function as an electrical generator without modification.  Any nanoblock design could contain some volume for miscellaneous functionality such as a few gates of digital logic, a fan-out of a control cable with signal amplification, or simply passing a signal through; reserved volumes that are continuous between various block faces would be especially useful.  A fourth class of block would contain just enough diamond for rigidity of faces and support of interior structure; this would be used mainly to contain predefined nanomachines in novel arrangements, or to support convergent assembly operations.  Miscellaneous functionality could be specified by direct design, or by semi-automated design using macros and automatic placement and routing.  (In constrained volumes automatic placement would be more difficult.)  Predefined blocks and block classes could be extensively tested.  Spatial separation of functional units, either within or between nanoblocks, will reduce unexpected interactions.  Thus, most if not all nanoblocks in a product will be pre-designed (or contain predesigned components arranged according to design rules), easy to specify, pre-tested, and highly reliable.
 

5.1.4. Patterns and Regions

The simplest pattern consists of a single nanoblock type, with faces compatible with stacking.  More complicated patterns may specify repeated or tiled arrays of different nanoblocks; these may be used to implement (for example) a material with embedded strain sensors.  Patterns may be one-, two-, or three-dimensional, and may be designed to stack either with themselves or with other patterns.  Pattern specification can be recursive: patterns can include smaller patterns or regions.  In the design of the nanofactory, each convergent assembly stage can be represented as a single pattern, consisting of eight copies of the sub-stage pattern, plus the walls, braces, and assembly tube required to connect them.

Patterns of nanoblocks can be tiled to form virtual materials occupying regions.  For example, a structural material could have a nanocomputer per cubic millimeter, connected into a 3D grid, and strain sensors embedded in various nanoblocks.  A design for a single display pixel could be tiled to form a raster display of any desired size.  A useful CAD program will allow such materials to be designed, and then used to fill specified volumes; by this method, large, simple products can be specified with very little design effort and small file sizes.  (In any case, the size of the specification depends on the complexity, and not the size, of the region.)  A more sophisticated program would allow the algorithmic specification of complicated volumes, such as fractal trusses.  The nanoblock width of 200 nm is 100 times less than a typical human cell (Freitas, 1999, table 8.17); for most human purposes, a material specified in terms of whole nanoblocks would appear smooth, but partial blocks could be made as long as the convergent assembly mechanism was still able to grip them as needed.  Some machinery such as large cylindrical bearings will be improved by partial nanoblocks; lining the bearing surface of each block with graphite sheets will smooth out any rough edges left by bulk diamond fabrication.  (See Section 3.2.2).  For convenience in packing products more compactly, a simple extension of the concept allows two different patterns to specify different fractions of a nanoblock's contents; this allows patterns to interpenetrate or to stack tightly, and can be used to specify small parts attached to nanoblocks during fabrication but removed during unfolding.

Although the volume of nanotech-built machinery is far smaller than the conventional machinery required to perform a comparable function, some provision for redundancy will be required above the nanoblock level.  For example, generating 1 W of mechanical power requires perhaps two thousand cubic microns of electrostatic motors, which may receive a damaging radiation hit every few days (see Section 8.5).  The process of combining functional modules into larger modules that are tolerant of radiation will be a common design pattern.  The larger modules can then be combined into a second-order virtual material, if desired.

During convergent assembly, the product is assembled from sub-blocks into larger blocks.  Thus a 10.5-cm product is assembled from 5.25-cm blocks, which are assembled from 2.635-cm blocks, and so on.  However, the boundaries of patterns, and of regions, need not correspond to the assembly boundaries.  With ridge joints, nanoblocks can be assembled simply by moving them into contact.  This implies that any pattern should be able to be split along any assembly boundary, or conversely, that assembly boundaries can fall anywhere in any pattern.  In practice, two difficulties arise which may require some accommodation of the assembly method, depending on the product.

Spaces within a pattern or around a region may be left empty of nanoblocks.  A void may cause an assembly failure because of a thin or unattached piece adjacent to an assembly boundary.  Voids do not pose severe problems for the nanofactory design.  The nanofactory, as fabricated, will not include large voids, since it will be unfolded after fabrication (see section 5.1.5).  In product designs requiring voids, the voids may be filled with a scaffold of mostly-empty nanoblocks that can fold out of the way after construction.

Another difficulty is that assembly of large blocks may not allow sufficient precision to use ridge joints only a few nm in size; it is not yet known whether two isothermal cm-scale diamond faces can be aligned within a few nm across their entire surface.  Patterns and regions may have to be defined to accommodate larger joining structures, either alignment pins as suggested in (Drexler, 1992, sec. 14.2.1b) or larger ridges.  The nanofactory structure is simple and repetitive; if larger joint mechanisms are necessary for the final few joints, they can be inserted into the design at many points.  The design can be stretched as necessary so that the large joining mechanisms fall in permissible places.
 

5.1.5. Folds

The nanofactory will be manufactured in a collapsed state and then unfolded.  The nanofactory consists of filled nanoblocks (computer components and fabricators), walls, bracing cables, and convergent assembly robotics of various sizes.  The fabricator arrays are all co-planar.  The interior of the production module is empty except for the first four stages of convergent assembly robotics.  Gantry crane robotics are basically linear, and can be folded more or less flat.  The nanocomputer face of the production module can be folded in half.  Similar manipulations are carried out for all factory components, allowing them to lie flat in a "crushed" configuration.  Note that a solid wall can be "crushed" without strain, since it is manufactured in the crushed position and the mating faces of the "crease" do not meet until unfolding is almost complete.

To visualize the initial collapsed configuration and the unfolding process, it may help to imagine crushing a finished nanofactory.  The factory is crushed perpendicular to the plane of the fabricator arrays.  The robotics inside the production module fold up, as do the bracing cables spanning the cooling channels.  The wall of computers, which is perpendicular to the crushing direction, folds in half.  As the crushing continues, the convergent assembly tubes running parallel to the crush plane fold along their length, and perpendicular tubes split along the edges and fold accordion-fashion.  The robotic equipment contained in the tubes was made of hollow girders or thin pieces designed to be easily crushable; it folds flat.  The large unused volumes of the factory adjacent to the assembly tubes are filled with a 3D network of tension bracing and/or a network of tubes to carry fluid across the gap.  This structure detaches from all but one or two of the walls and collapses in on itself.  When the factory is as flat as possible, it is then crushed from the sides.  The production modules are already as compact as they can get.  The tubes that were accordioned now buckle, and the structures in the adjacent voids compress further.  The tubes and other structures form layers only a few nanoblocks thick over blocks of mostly solid fabricators and computers.  During the unfolding, this hypothetical process is reversed.  Since functional connections are all press-fit, and ridge joints require only to be pushed together, connections can be formed during the unfolding process as blocks come into contact.  As long as the unfolding mechanism is capable of aligning the joints properly (note that guides can be used for final alignment), the nanoblock joining process during the unfolding stage is as simple, flexible, and reliable as during the convergent assembly stage.

Thus each production module and assembly tube will be constructed in a collapsed configuration, and unfolded/expanded after construction.  Note that convergent assembly boundaries do not have to be aligned with tube, substage, or module boundaries; a subcube may contain part of a module and part of a tube, to be joined with the corresponding parts during a later convergent assembly stage.  As constructed, some wall junctions will be hinged together, and some will be initially open but will join as the factory expands.  As discussed in (Drexler, 1992, sec. 11.4.2), unbonded diamond surfaces pressed together can exclude even helium.  Larger nanofactory structure--large assembly tubes, cross-bracing for voids, and exterior panels--can also be constructed in a collapsed state.  Interior cross-bracing for large pressurized volumes must run in three orthogonal directions, attached to six walls.  During construction, it will be fastened to two opposite walls which are collapsed together, with the other four walls folded away from it.  As the walls are pulled apart, the bracing expands, placing ridge joints attached to it in the right position to meet the other four walls as they move into position.  More bracing will be required in wider voids, which will be adjacent to larger tubes with bigger robotic components.  Any remaining gaps can be filled with hollow nanoblocks to facilitate assembly handling.  If the nanoblock volume is slightly larger than the fabricator volume, then the adjacent module components (the bracing on one side of the fabricator wall and the robotics on the other side) can be compacted into the same nanoblock as the fabricator; this would allow a collapsed production module to be only two nanoblocks thick.  Alternatively, the adjacent module components might be constructed to one side of the fabricator planes, and inserted and joined during the unfolding process.

For many products, the unfolding stage can be quite simple, or even unnecessary if the finished size is smaller than the factory's volume capacity.  However, the process may be arbitrarily complex if the parts require substantial rearrangement in order to form the finished product.  This is not a severe limitation on most products, since unfolding complexity can usually be traded for larger manufactured volume.
 

5.1.6. Networks

In products, it may sometimes be necessary for several functional networks to interpenetrate the same volume.  Identical networks can be offset by a certain displacement to avoid collision; however, networks may be of different scale, topology, or even character--one may be fractal and another gridded.  As long as the containing volume and cross-sectional area are much larger than the volume and area required for network functionality, and the network specification contains rules for bending channels, the problem will probably be locally solvable.  Once a nanofactory exists, the amount of computing power required to verify the existence of a solution in every crossing point in a design will not be expensive.  A class of nanoblocks may be defined with volumes reserved for networking connections to be filled in by the CAD software.  (W. Ware suggests, by analogy with FPGA's, the use of nanoblocks whose function is "programmed" by a set of actuators to make or break various mechanical or electrical connections.)
 

5.2. Simulation and testing

5.2.1. Design and simulation

Digital hardware design provides an example of the effects of design cycle time and cost on simulation effort.  An ASIC (application-specific integrated circuit) is a kind of chip that can contain very complex and fast circuitry; it is custom-designed for each product.  Once simulation is completed, an ASIC may take several months and thousands of dollars to construct, and it may be useless if it does not work perfectly.  A team of ASIC designers will frequently spend months simulating their design before beginning production.  An FPGA (field programmable gate array) is similar to an ASIC in complexity, but is general-purpose and programmable: its design is specified by a file that is loaded each time the power is turned on.  Changing the functionality of an FPGA requires only a few seconds.  As a result, an FPGA designer may not do any formal simulations at all, preferring to simulate mentally during the design process, find problems during testing, and fix the problems in a subsequent design/compile/load/test cycle.

Simulation of the behavior of individual atoms requires specialized, computation-intensive techniques.  These techniques are rapidly being developed, but their correct use still requires specialized training, and it is probably safe to say that most product designers will not find quantum chemistry intuitive.  Nanoparts, and some nanomachines, will have to be simulated extensively to ensure that they will not break under unexpected use, and to develop a suitable mechanochemical manufacturing process.  This will have the effect of keeping the number of different nanomachines small.  However, a variety of different nanoblocks can be built from only a few nanomachines.  Only a relatively small palette of nanoblock classes, implementing a few basic functions, will be required to build a large range of products.  Even for components smaller than a nanoblock, simulation may be simplified by the use of simple, well-understood mechanical structures such as diamond lattice: diamond shapes larger than a few nanometers should have properties nearly equivalent to those of bulk diamond (Drexler, 1992, Sec. 9.4).  To the extent that simulation is necessary to test a nanomachine assembly sequence, a simple rigid-body simulator will usually be sufficient.

Although few or no additional mechanochemical techniques will be necessary to bootstrap a nanofactory from a working fabricator or to build a wide variety of products, the performance of the nanofactory and of some of the products can be increased as new chemistry is developed.  Much of the new chemistry will be localized, and simulable in standard chemical packages.  However, at least one useful class of device, bearings with strained shapes and lattice dislocations, will probably require both chemical and mechanical simulation.  This is beyond the scope of this paper and requires further study.  Several classes of bearings have already been analyzed (e.g. Drexler, 1992, chap. 10; Merkle, 1993) although mechanochemical fabrication sequences have not been proposed.  A proposed molecular planetary gear has already been tested in simulation (Cagin et al., 1998).

A well-designed nanoblock will have a simple, well-understood function.  Once a nanoblock has been designed, simulated, and tested, higher-level design and simulation systems can work with its simple functional characteristics (including volume and surface) instead of its complex chemical construction.  Humans will be able to comprehend the function of basic nanoblocks, so will be able to design simple products without requiring formal simulation to verify correct functioning.  With a working set of predesigned nanoblocks (including standard inter-block connection arrangements), product designers will not need to design new nanoblocks for most new products.  As with standard libraries in programming languages, designers will become comfortable with available functionality, and will be discouraged from developing new low-level functionality by the difficulty of learning to use it, as well as the difficulty of designing it.  Many of the tools required to design the initial set of nanoblocks will be developed in the course of developing the fabricator device, and thus be available for preliminary product design even before the nanofactory is bootstrapped, but product designers will work more efficiently if they don't have to design new nanoblocks.  For the initial nanofactory, it should be possible to have different groups engaged in developing the nanoblocks and integrating them into the nanofactory design.

The mechanical aspects of the convergent assembly process usually will not need to be simulated in detail.  The block faces, including ridge joints and functional joints, must mate properly, and at least one other face must allow adequate gripping for the required assembly manipulation.  Verifying these conditions requires only static analysis, not simulation.  A very flimsy block may sag or twist enough to misalign the joint ridges, or may include loosely connected pieces that could jam the alignment due to vibration or other unexpected force.  Conservative design rules and static analysis can avoid such problems; simulation can allow less solid design.  The order in which blocks are joined will not be important, since blocks are joined simply by pushing them directly together, and the rectilinear planar faces will align to produce flat faces in the resulting two- or four-block intermediate shapes.

The process of unfolding the product may benefit from rigid-body simulation.  For relatively simple designs, lack of simulation usually will not be a problem.  The simulator may need to account for van der Waals forces to ensure that part separation occurs properly.

As discussed in Section 8.4, construction of nanoblocks and of products made from nanoblocks may be quite rapid.  If a prototype can be produced in a day or less, simulation of products may not be a large part of the design cycle; as in software (or FPGAs), good design methodology will enable the construction of quite complicated systems, and simulation or formal proof of correctness usually will not be worth the effort.  This is a mixed blessing: we may anticipate that nanotech products with complexity equivalent to modern software applications will contain comparable levels of bugs.  However, it should be noted that most of the physical products in use today are far less complex than modern software applications.

Any complex product will probably need to be tested and debugged at a high level, and both of these tasks may be easier in simulation than in the actual product.  Simulators that can handle mechanics, electrostatics, and surface forces have already been developed for MEMS applications (Algor, Inc., 2003).  Simulators and emulators for digital logic have been in use for decades.  A desirable feature would be a generalized ability to formally specify a desired behavior for a nanoblock or other subpart, test the specification by simulating that part, and then use the same specification in a higher-level simulation.
 

5.2.2. Testing and debugging a nanofactory-built product

Any product needs to be tested after it is built, to find errors in design or construction.  The high reliability of the manufacturing processes will minimize the number of construction errors, and the simplicity of function of the component nanoblocks will reduce the number of design errors.  In general, a product will fail because of problems analogous to software bugs.  If not weeded out in the design stage, these can usually only be found by testing the functionality of the product as a whole.  Nanotech can neither help nor hinder this process, except by allowing a large fraction of the product to be devoted to small integrated diagnostic devices.  Errors in the nanotech-built structure will be few, and many of them will be deducible from the function, just as a software engineer can diagnose a design error in a computer chip by observing its outputs.  With the active components being a small fraction of most large products, there will be ample space for isolating components from each other, preventing unexpected physical interactions.

A computer chip may contain millions of transistors, and a computer program may contain millions of instructions; both of these are far more complex, more sensitive to propagating errors, and more opaque to debugging efforts, than any mechanical design is likely to be (with the exception of designs intended to perform as computers, which can be handled with adaptations of today's hardware and software design methods).  Diagnostics are extremely useful in software to verify the correct functioning of small pieces of the code.  Diagnostic testing of individual pieces of hardware design, including statistical testing by fabricating large numbers of copies, will surely be useful.

Direct inspection may be helpful in some cases.  A means of selectively withdrawing shims from ridge joints would allow the product to be split open for inspection along any 200-nm plane in any of three orientations.  Parts too small to be seen optically could be studied with an electron microscope or scanning probe microscope.  One company claims to be developing an optical device capable of producing 3D images with resolution <10 nm (Olson, 2002), but as of this writing the company is not yet publishing details or demonstrating product.  Finally, most human-scale products will consist largely of empty space which can be filled with monitoring equipment in experimental product versions.
 

6. Control of the nanofactory

6.1. Nanocomputer architecture and requirements

Data passing between adjacent nanoblocks can be done via a mechanical pincushion; a block face has room for thousands of 1-nm logic-rod interfaces.  The stiffness of a van der Waals interface is equivalent to 30 nm of diamond (Drexler, 1992, sec. 9.7.1), probably acceptable for this application.  Both strength and stiffness can be improved at only slight cost in mass by making the interface area larger than the cross-section of the rod.  Coprocessors, memory, or specialized hardware can thus be added to the basic CPU without having to fit into the same nanoblock.  For long-distance signaling, sheathed polyyne rods are adequate for distances of a few microns (Freitas, 1999, sec. 7.2.5.4); longer distances can use thicker rods and slower speeds, or electrical signals.

RAM requires up to 40 nm^3 per bit, and error detection requires 9 bits per byte, so a 200-nm nanoblock can hold at least 20,000 bytes.  Mass storage devices are not assumed for the lowest-level (production module) computers due to the intensive use of DMA (direct memory access) to control the fabricators.  A gigabyte of RAM would require 50,000 nanoblocks (~7 micron cube, within range of polyyne signaling).  A modest 20 megabytes would require 1,000 nanoblocks, which can be arranged in a single layer ~7 microns across; if this is insufficient in practice, additional layers can be added without concern for energy use or cooling since the RAM is static and requires very low power.

The large amount of RAM used by the chosen architecture requires a means of dealing with radiation-induced errors.  Correction of a single bit error can be done by adding 8 bits for every 64, and requires decoding circuitry that may slow access but will not add significantly to the volume (Kozierok, 2001).  Depending on the spacing of damage from a single radiation hit, it may be necessary to physically separate the bits so that one event will not damage more than one bit.  Within a single nanoblock, 72 bits can be separated by 40 nm; greater separation requires splitting single memory entries among multiple nanoblocks, which complicates the design of DMA controllers.  Although multiple hits to the same RAM block are possible, multiple hits to the same memory word are extremely unlikely (<10^-14 per year; see Section 8.5) because each word involves only ~3000 cubic nanometers of machinery.  In designs for high-radiation environments, massive reliable parallelism, or extreme lifetimes, the contents of the memory word can be moved to a different location when the first hit is detected.  (Detection requires timely reading of each memory word, at slight additional power cost.)  The requirement to separate the bits may require additional motion (and thus power dissipation) to read a word.  This can be compensated by slowing the access speed--a cache will probably be in use anyway--or arranging multiple consecutive words to be accessed with the same motions.

CPUs contain a large amount of heterogeneous circuitry, so adding error correcting circuitry may not be straightforward.  The simplest solution is to run three CPUs in parallel, reading from a single memory interface, and compare their outputs.  This allows detection of errors even after one CPU is damaged.  For longer lifetime, more CPUs could be added, but only a fixed number would need to be running at any one time.  When a failure was detected, the state of a good CPU could be copied into an idle CPU (similar to saving and restoring state during an interrupt), the failing CPU shut down, and the new CPU started.  The chance of a second failure happening before the state could be copied is remote but possibly significant in highly parallel designs.  Of greater concern is the possibility that a single radiation event could damage two CPUs.  Such a failure would almost certainly be detected, but it might not be possible to tell which CPUs were damaged unless four were running.  A more efficient design that can be used with write-only I/O hardware (Section 8.2) uses only two running CPUs, so errors can be detected immediately but not corrected.  Instead, the program is divided into checkpoints, and the runtime is tracked.  When an error is detected, the program is re-loaded into backup CPUs from the last checkpoint, and the I/O of the CPU is disabled until it reaches the point at which the error occurred.  This solution will be used for the production module CPUs, requiring ~60,000 zJ per instruction.
 

6.2. Placing the nanoblocks

Decoding this part of the specification is easy.  The product volume is divided into regions, and any sub-volume is specified by sub-patterns and sub-regions down to the individual nanoblocks.  Any point in the product corresponds to a single nanoblock, and each fabricator in the factory corresponds to a single position in the product and is used to build a single nanoblock.  (This relationship may change due to radiation damage, but only within a single production module under control of a single computer.)  The process is fully parallelizable: decoding any position does not require information about any other position.  The volume specification is broadcast to all production modules, in order of size from the largest region to the smallest pattern.  To determine which nanoblock is to be made by a particular fabricator, the module's computer selects the appropriate region, sub-pattern, sub-region, and so on, according to the location of the fabricator's nanoblock.  Each selection is simply a solid geometry calculation.

Since the boundaries of the regions are not limited by the boundaries of the product blocks and sub-blocks, a region may cover a large number of production modules.  Also, since a nanoblock design may be used throughout the product, the design may have to be sent to a large number of production modules.  For some products, it may be worth keeping track of which parts of the nanofactory a given nanoblock design should be sent to.  However, this would require additional algorithms and a hierarchy of additional computers in the nanofactory, so is not used here; all details of the design are broadcast to every production module.  After the pattern and region information has been broadcast, the nanoblock information is broadcast.
 

6.3. Specifying the nanoblocks

If the fabricator is mechanically controlled by discrete pulses, it can be driven directly by the rod-logic system.  Even in Merkle's admittedly inefficient assembler design, the energy required by a fabricator actuator is comparable to the energy used to drive a rod-logic element; thus, it is likely that amplification will not be required to drive actuators directly from rod logic.  (In rod logic the energy used is mostly recoverable (the operation is reversible), while in actuation the energy may not be recoverable.  This does not require any design change to the rod-logic hardware.)  The pulses can be produced by interpreting the control words produced by the decoding logic.  A simple coding divides a sixteen-bit word into one mode selection bit and fifteen line selection and counting bits.  The first mode uses six bits of selection and nine bits of power pulse counting, allowing up to 512 pulses to be sent to any of 64 single control lines.  (Where the pin drive (Section 3.1) is used, a pulse will be translated into several consecutive operations, all of them thermodynamically reversible except perhaps for the main shaft motion.)  The second mode provides four bits of sub-mode selection to guide the division of the remaining 11 bits into multiple counting fields and the assignment of those fields to control lines; this allows short operations to be done concurrently by pulsing multiple lines simultaneously or in sequence with separate counts, in any of sixteen hard-coded combinations.  Some of the sixteen modes can be used to specify interleaved actuation of several robotic degrees of freedom (e.g. tripod legs), permitting motion at an angle.  Merkle estimates that placement of an atom may require on the order of 1000 pulses; this accomplishes large tripod motions and detailed mechanochemical work, and also includes control line selection.  A large tripod motion may require six words, one for each leg, for each motion.  Detailed work will not require many pulses, and with careful design of the second mode codes, can probably be accomplished with only a few words per operation.  Thus it is reasonable to estimate that each atom placed requires 25 words (400 bits) of control codes.  These 25 words can be generated by special-purpose decompression logic to minimize data transmission and storage requirements.

Special hardware logic for decompression can implement fairly complex functions, including accessing multiple tables in memory and doing arithmetic on the values retrieved, far more efficiently than a general-purpose CPU.  Most of the decompression operations, including arithmetic operations, could be implemented in reversible logic, saving significant energy.  For example, adding hydrogen atoms to a flat diamond surface is likely to be a very repetitive operation; the only thing that changes from atom to atom is the distance moved to reach the next attachment position, and the atoms are in a regular pattern.  The decompression logic would have to combine information from three or four sources.  One is the list of instructions common to all hydrogen addition operations.  The second is tables of positional offsets specifying individual atoms in a two- or three-dimensional crystal cell; the cell can include a large number of atoms.  The third information source is numeric constants representing the starting position of the cell.  Thus a few numbers can invoke the placement of dozens or even thousands of atoms, depending on the size of the cell tables.  J. Soreff points out that the precomputed positions may require slight additional tweaking to compensate for varying surface strain near workpiece edges.  This can probably be precomputed and stored in additional tables, supplying a fourth source of information.  Although significantly more complex than a standard DMA (Direct Memory Access) controller, the logic required is well within the capability of existing digital design methods (significantly simpler than a JPEG decoder, for example) and requires only a few registers and adders to implement.

In the nanofactory, all nanoblocks other than the mechanochemical fabricator will be composed mainly of bulk diamond, graphite, and other simple materials, allowing the use the efficient DMA hardware as described above.  Only a few kinds of atom-placement operations will need to be done, so only a few operation lists will be stored locally for repetitive delivery.  The size of cell tables can be chosen for optimal tradeoff between the local memory used and the amount of data distributed to invoke the tables.  The contribution of the production module's CPU to mechanochemical operations is simply to allocate local memory to store the parts of the broadcast instruction streams that are relevant to the nanoblocks it is building, and program the local DMA/arithmetic hardware to send the instructions on to the fabricators.  This requires far less than one CPU operation per mechanochemical operation.  Note that any sequence of operations that cannot efficiently be generated by cell tables can be delivered directly in control code sequences.
 

7. Product Performance

In products, distribution of liquids can take place through pipes that are simply implemented as holes in diamondoid structures.  Hydrogen-terminated diamond should be unreactive to most of the fluids that might be used, or the holes can be lined with graphite.  Distribution of electricity can take place through graphite inclusions in the nanoblocks that are pressed together when the nanoblocks are joined.  (In some configurations, buckytubes can be excellent conductors of electricity, though in-plane conduction in graphite will be adequate for many purposes.)  Power can also be transmitted in the form of mechanical motion; a  rotating rod 10 nm in diameter can transfer 1 mW of power (Freitas, 1999, sec. 6.4.3.4).  This is small enough to be included in any part of the design, and far more power than is needed for a nanocomputer (7.5 nW) or mechanochemical fabricator (150 fW).  The rod need not be supported along most of its length, reducing frictional losses.

For transmission of digital information, the breaking strength of a polyyne rod is far higher than the force needed for reliable transmission of information, so a single rod can be used to pull several rods in a broadcast architecture.  Electromechanical repeater stations can also be used, in which the motion of a rod switches electricity to actuate another rod with increased force.  Finally, signals can be sent electrically, by pulses in graphite "wires" which can be subdivided.
 

7.1. Strength, stiffness, and shape

The shape of the product will be limited by the convergent assembly mechanism, but the possible final shapes are increased by the ability to unfold the product after assembly and securely join the result.  Even during assembly, the product need not be a solid cube.  At each stage, the convergent assembly mechanism must be able to manipulate each sub-block and position it precisely for joining to its seven neighbors.  However, the surface area required for a secure grip is quite small: the weight of the largest sub-block is about 5 N, requiring less than a square millimeter of van der Waals contact to hold it against gravity, so faces need not include much contact area for manipulation.  A design process might involve designing a final product shape containing large empty volumes, then simulating "crushing" the shape until sufficient pieces touch to support the convergent assembly process.

The nanofactory may have trouble assembling products in which a very small fraction of a large block is filled (adjacent to a block that it will join at a late stage in the convergent assembly process).  The tiny piece may be too small for the larger manipulators to handle.  In general, such small pieces can be either relocated, omitted, or surrounded by lightweight scaffolding to allow handling by large-scale manipulators.
 

7.2. Appearance

7.3. Complexity

The construction method imposes no penalty for high precision no matter how many parts are specified--the only cost is design.  Thus a nanotech-built product can contain more than a billion times as many parts as the same volume of conventionally manufactured machinery or electronics.  This many parts cannot be individually designed.  To a large extent, the functional power of a nanofactory-built product design will depend on the sophistication of the design software and on the development of a useful library of virtual materials.  In the near term, there are many applications where a repetitive, small-scale design is useful, including visual displays, massively parallel computers, combinatorial research (testing many variations on a theme),  many medical applications, and the nanofactory itself.
 

7.4. Design

7.5. Powering the product

Efficient conversion of chemical energy into other forms requires special mechanochemical apparatus, which is not assumed here.  A fuel cell may be the best short-term solution.  Freitas  (1999, sec. 6.3.4.5) analyzes a 40% efficient fuel cell producing up to 2 pW/nm^3 (10^15 W/m^3) in its active region, although his design involves oxygen-terminated diamond.

A lightweight solar energy collector, consisting of a holographic lens or water-filled Fresnel lens concentrating sunlight onto a diamond thermionic cell (Salisbury, 2001), should be able to
recover the energy cost of its manufacture in only a few days.  A square mile of desert land receives on average more than 500 MW of solar power (including night and seasons), and
thermionic conversion should be ~50% efficient.
 

7.6. Computation

The fastest computer in the world, as of this writing, is the NEC Earth Simulator (Top500.org, 2002).  It includes 640 8-processor nodes using 20 kW apiece, for a total of 13 MW (ignoring the large crossbar switch).  It also includes 10 TB of RAM, and fills a large building.  Assuming that the Earth Simulator's power consumption per operation is comparable to the Pentium 4, a massively parallel nanocomputer with equivalent raw processing power would require 2 watts.  The CPUs would require a volume of 8 million cubic microns, and the memory an additional 3 million cubic microns.  The entire computer could fit into a cubic millimeter.
 

8. Nanofactory calculations

Because many of the calculations are repetitive and tedious, a computer program was used (Appendix A) to calculate some of the results.  The methods of calculation are explained in the text, except for certain numerical techniques that are explained in the program.

For convenience, a specific nanofactory size is chosen as the basis for several parameters: a tabletop design that can produce ~4 kg of diamond (~10.5 cm cube) in a few hours.  This product size is 2^19 times the length, and 8^19 times the volume, of a nanoblock.  Thus 19 convergent assembly steps are required to fabricate the product from 1.44x10^17 nanoblocks.
 

8.1. File size and data distribution

Aside from the larger convergent assembly robotics, for which each part must be specified in terms of solid-geometry regions, the entire nanofactory design will require only a few hundred patterns and regions, all of simple shape, based on just a few nanoblock designs.  This will require very little information to describe.  Of course, this only specifies the placement, not the contents, of the nanoblocks.  The contents are specified by direct description of the mechanochemical and assembly operations needed to fabricate them.  Since a nanoblock contains up to 1.4 billion atoms, and an atom requires up to 25 words (50 bytes) to specify, a complicated nanoblock design might require up to 70 gigabytes.  In the nanofactory, all nanoblocks except the fabricator will be relatively simple and repetitive, being built entirely of bulk diamond, and even the fabricator will include large volumes of regular structure.  (The nanocomputer blocks will involve complicated machinery, but built from just a few small digital logic components.)  Thus in the worst case, the nanofactory file size may be perhaps a terabyte.  A more reasonable number is 100 gigabytes, and as little as 10 gigabytes seems plausible, but the nanofactory design can easily accommodate a terabyte or larger file.  Detailed specification of modern computer chips may generate files over a gigabyte in size, although these files can typically be compressed to 100-200 megabytes (Morrison, 2002).

The entire specification must be broadcast to all the production modules once per product cycle.  This requires sending perhaps 10^12 bytes over 1.6x10^8 meters.  A product cycle time of three hours (see Section 8.4) would require a bit rate of ~0.7 Gbit/s.  Since most of the distance occurs in the Stage 1 tubes, which are only 25 microns long and may have walls <200 nm thick, rod logic appears best.  (Coaxial electrical cable appears attractive (Freitas, 1999, sec. 7.2.5.1), but submicron coax has not yet been sufficiently investigated.)  The energy dissipated by a moving logic rod depends on its length and on the switching time; inspection of the equations in (Drexler, 1992, sec. 12.3.4) indicates that if the product of length * time is held constant, the dissipated energy should remain constant or decrease for each source of loss.  Equation 12.19 is an apparent exception, but a correction for thermal equilibration time was omitted in its derivation (sec. 7.4.1).  In other words, a rod-logic rod can be lengthened without increasing dissipative losses as long as its switching time is proportionally slowed.  An overly long rod will suffer positional uncertainty, but according to sec. 12.5.4a a 2x2-nm rod five microns long is adequately stiff for reliable operation.  A 1x1 by 64-nm rod loses 2 zJ per 0.1-ns switching cycle (sec. 12.3.8b).  Quadrupling the rod area increases vibrational losses (Equation 12.15) by approximately a factor of four; this term then dominates the dissipated energy.  Given the number of arbitrary design parameters, exact calculation is pointless; as will be seen, the energy used for instruction broadcasting will make negligible difference in the overall energy use of the nanofactory.  A conservative value of 6 zJ per bit per rod is used.  Partitioning a rod requires a register at each division, dissipating ln(2)kT per bit or 2.6 zJ at 273 K.  A rod-logic chain divided at 5-micron intervals will cost 1.7x10^6 zJ per bit per meter, and have a transmission rate of 128 Mbit/s (and a delay of ~1.5 ms/meter, which is unimportant in this design).  With these arbitrary but conservative parameters, 6 rods working in parallel can carry the desired 0.7 Gbit/s, and the cost per bit for factory-wide broadcast is 2.8x10^-7 J; a 10^12 byte file requires 2,200,000 J, or only 611 Wh, or 11 zJ/atom for a 4 kg product.
 

8.2. Fabricator control, energy, and cooling

Data distribution to production modules, as we have seen, requires very little energy.  Local data processing requires quite a bit more.  The redundant nanocomputer system described in Section 6.1 uses 60,000 zJ per instruction, but the use of efficient DMA controllers allows many atoms per instruction to be placed.  As estimated in Section 6.3, placing an atom may require 400 bits to be sent from the nanocomputer's memory to the fabricator, an average distance of 8 microns.  Placing 1.4 billion atoms (200-nm cube) in 3 hours (see Section 8.4) requires a data rate of 50 Mbit/s.  Following the calculations in Section 8.1 (with suitable adjustments to extend rod length beyond 5 microns) the energy required is about 2000 zJ/atom.  However, it will be possible to reduce this by any fraction desired, by using more and slower rods; a bundle of 81 2x2 nm rods to control a column of 81 fabricators requires only 18 nm square.

The internal hardware of the fabricator will dissipate energy through friction.  Without a detailed design, this dissipation cannot be reliably estimated.  However, it should be noted that the moving components are on a scale comparable to rod-logic elements; that only a few components will be moving at a time; and that their speed will also be comparable to the speed of the driving rods.  It is plausible that the fabricator may require significantly less energy to overcome internal friction than is used to deliver its control pulses, ~2000 zJ/atom.

Energy that is stored in the system as work (as in compressing a spring) can be recovered when the actuator is moved backward.  The force of the spring will drive the actuator backward, imposing a force on the driving system.  If the driving system is capable of generating potential energy (running in reverse), the energy can be recovered.  Drexler's electrostatic motor has this capability.

Energy dissipated in abrupt state transitions cannot be recovered.  Examples of state transitions include erasing a bit, pushing a ratchet past a tooth, and pushing a component past a soft projection that springs back suddenly.  Since the state of the fabricator's mechanism and workspace is predictable at all times, no energy needs to be dissipated within the fabricator to keep track of it; the digital logic control eliminates any need to retain state internally.  Its operation will require no irreversible state transitions.  The pin drive described in Section 3.1 allows a stepping motion to be produced without any use of ratchets.  The digital logic control can change states without abrupt energy transitions, while retaining its state reliably in the face of thermal noise.  This permits operation orders of magnitude more efficient than (for example) the Merkle assembler, which requires large amounts of energy to operate ratchets and to overcome thermal noise.  Although accidental state transitions can be eliminated from a good nanoscale mechanical design, it is unknown at this point whether such problems will exist in the preliminary fabricator design.  In general, abrupt state transitions can be avoided in stiff sliding machinery.  It may be hoped that the designers of the fabricator will have worked to eliminate them.  However, this may not be the case in early designs.

A chemical bonding event may act as either a reversible spring or a sudden state transition, depending on the stiffness of the driving mechanism.  If the chemical manipulator and all drive systems could be made sufficiently stiff, this chemical energy could be recovered like any other stored energy.  The high forces encountered during mechanochemistry may not be easy to overcome; if they cause the manipulators to "snap" from one position to another, the corresponding energy will be lost.  The cost of inefficient chemistry must accordingly be included in the energy budget.  A tetravalent carbon atom has a bond energy of approximately 556 zJ/bond (the number varies depending on the surrounding chemistry) or 1112 zJ/atom since each atom forms four half-bonds.  This number may be multiplied by a small factor if multiple chemical steps are required to prepare an atom or molecule for deposition.  On the other hand, the feedstock molecule may include several atoms already bonded appropriately, which could save a large fraction of the energy.  In the absence of complete information about feedstock chemistry and processing, 1000 zJ per product atom is taken as a reasonable estimate for the cost of mechanochemical operations.

The drag forces generated by rapid movement through gas at atmospheric pressure may be significant even for small devices.  In Merkle's design, the tripod moves perhaps 100 nm to place an atom in 0.1 msec; this implies an average speed of 0.001 m/s.  With a viscosity of 2.1x10^-5 kg/(m s) for argon (neon is 40% higher) (Handbook of Chemistry and Physics, 1971), the power required to move a single 10-nm diameter sphere (Stokes drag times velocity) is 2x10^-18 W (Freitas, 1999, sec. 9.4.2.4) or 0.2 zJ per atom.  However, the power scales as the square of the velocity; faster fabricator speed or jerky motion may increase this number significantly.  In addition, smaller parts may move at speeds of 1 m/s or more.  To be conservative, the working area of the nanofactory (as opposed to the coolant channels) is assumed to contain either hard vacuum or inert gas at low pressure.  (Nanofactory structure to withstand collapse from internal pressure differences is considered in Section 8.3.)

The above energy figures cannot be summed to give a meaningful answer, since some of them depend on engineering choices and others depend on unknown aspects of fabricator design.  However, it appears possible that the energy spent per atom can be limited to around 4000 zJ for frictional losses, 1000 zJ for mechanochemical losses, and perhaps another 1000 zJ for computation (if each production module computer runs full time).  These estimates are not especially brittle, since each of these losses (with the possible exception of mechanochemistry) can be controlled by engineering.  Accordingly, a cost of 10,000 zJ per atom is taken as a reasonable, conservative estimate for further calculations.  Since 1 kg of diamond contains roughly 5x10^25 atoms, the energy cost per kg is 5x10^8 J, or 140 kWh.  A factory producing 4 kg in 3 hours might need to dissipate approximately 200 kW.

A coolant consisting of suspended encapsulated ice particles can absorb 1.2x10^8 J/m^3 (Drexler, 1992, sec. 11.5), so less than 2 liters per second of this coolant would be required.  This will be divided among many linear channels.  Figure 5 shows small 1x16 micron coolant channels left open in Stage 1.  As Stage 1 components are stacked to make larger stages, the channels line up and form long narrow linear (non-fractal) pipes.  For laminar flow, the pressure required for a certain flow rate is directly proportional to the length of the pipe and to the velocity of the fluid.  The volume of coolant in the pipe must be replaced in constant time regardless of pipe length, so the necessary coolant velocity is also proportional to the length of the pipe.  Thus the pressure required to cool the pipe is proportional to the square of its length.  Running sufficient fluid to cool 16,384 production modules through a 40-cm long 1x16-micron pipe would require quite high pressure.  However, splitting the factory into N independently-cooled slabs reduces the pressure by N^2.  Splitting into slabs requires only extending a few of the assembly tubes, not rearranging any of the internal architecture.  The formula for pressure drop from incompressible laminar flow through a rectangular duct of dimension 2*a by 2*b (where a is larger), from (Tunkel, 2002), is:
pressure drop =  3*v*L*V/(a^2*(1-192*a/(pi^5*b)*tanh(pi*b/(2*a)))), where v is viscosity, L is duct length, and V is average velocity.
Assuming a 200 kW cooling load, flow sufficient to cool 2048 basic modules in series can flow through the pipes with a speed of ~1 cm/s (laminar flow; Reynolds number near 1) and a pressure drop of ~6 atm.  See Appendix A for calculations.  Thus the factory may be split into as few as 8 slabs, with each slab supplied at the top and bottom by low-pressure coolant.  The energy cost for recycling (cooling) the expended coolant will be only a fraction of the energy input.

Transmitting 200 kW electrically requires high voltage and large conductors.  Within the factory, or even for input into the factory, mechanical transmission may be preferable; for example, a single rotating rod of 140 micron diameter could theoretically transfer 200 kW (Freitas, 1999, sec. 6.4.3.4).  Electrical and mechanical power can be converted in several ways.  A rotating electrostatic motor based on Drexler's design (Drexler, 1992, sec.11.7) can be built out of only carbon and hydrogen.  Bulk diamond is an excellent insulator, but a thin layer of diamond can be a semiconductor, and graphite is an adequate conductor.  The electrodes for such a motor should have varying work functions for simplicity and efficiency.  The work function of graphite is 4.5 eV, while the work function for CVD diamond has been measured at 5.7 eV (Groening et al., 2003).  This difference should be sufficient to place ~1 electron per (graphite) electrode in a motor similar in scale to Drexler's (50 nm).  With electrode charge and discharge driven by work function, the motor functions as a generator without modification.  With half the current carrying capacity of Drexler's design, its power density is only half of the 10^15 W/m^3 computed by Drexler; half a cubic millimeter suffices to convert 200 kW.

Electromagnets do not work well at small scales, but an electrostatic replacement for a solenoid can be made simply by charging parallel movable plates; a device about 12 nm can develop a force of 1 nN over a stroke distance of 1 nm by applying 5V (Drexler, 1992, sec. 11.6.4).  This is approximately as much work as is done by the pistons in Merkle's fabricator.  Likewise, an electrical pulse may be generated by manipulating the plates or dielectric of a capacitor, or by bringing a single charged plate (which may be charged triboelectrically) near a conductor.
 

8.3. Physical arrangement and mass

To produce eight 3.2-micron blocks requires a gathering stage of four production modules grouped around a 3.5-micron tube ("Stage 1" in Figure 5).  The dimensions of this are about 36x25x16 microns.  To produce eight 6.4-micron blocks, four stage 1's are stacked on each side of a 7-micron tube, for stage 2 dimensions of 61x65x36 microns.  The final factory is about 94x92x41 cm, not counting exterior panels; for intermediate calculations, and volumes and lengths, see Appendix A.  The final eight blocks are either assembled within the final tube and extruded, or a balloon is used for external assembly (Section 4.4).  A minimum-volume arrangement may not have space for simultaneous assembly of 8 blocks in the tubes of several of the smaller stages, so four blocks may have to be assembled and passed on to the next stage, and then the other four assembled; this adds only fractionally to the total product cycle time.

The nanofactory consists of low-pressure working volume surrounded and interpenetrated by higher-pressure cooling channels.  Small cables strung across the cooling channels, perpendicular to each surface, will resist the force efficiently.  The cable mass required is directly proportional to the volume and the pressure, and inversely proportional to material strength; surface area and configuration can be ignored as long as the configuration is rectilinear.  Thus the amount of tensile bracing required to maintain structural integrity in the factory will be directly proportional to the amount required to maintain the structural integrity of a hypothetical cubic-meter box pressurized to one atm.  One atm of pressure exerts ~100,000 N of force per square meter.  Holding opposite faces together in a 1-m cube pressurized to 1 atm requires 100,000 N.  A cable with the density of diamond and a conservative tensile strength of 5 GPa (5% the strength of diamond) needs a cross section of 2x10^-5 m^2, and of course will be one meter long.  Three cables are needed (one for each pair of faces) for a total volume of 6x10^-5 m^3 and mass of 210 g for the hypothetical one-meter one-atmosphere cube.

The volume of cooling channels can be calculated by subtracting production module and tube size from total factory size.  The production modules occupy a total volume of 0.055 m^3 (~47 times the volume of their product).  The volume of assembly/delivery tubes is 0.066 m^3, for a total volume of 0.12 m^3.  (See Appendix A.)  The volume of the nanofactory is 0.35 m^3, so this volume is about 1/3 occupied, leaving gaps totaling 0.23 m^3.  These gaps will be filled with coolant under pressure, and this pressure will try to collapse the factory's workspaces and must be resisted.  The design arbitrarily limits coolant pressure to <10 atm.  To withstand this pressure in the 0.23 m^3 open volume of the nanofactory requires 0.28 kg of bracing material (0.21 x 10 x 0.23).  Inspection of Figure 5 shows that some coolant channels will be blocked by assembly tubes in stages divisible by 3; this requires a <1 micron gap between the sub-stages and the tube, which is not included in the present calculations.  It may be desirable to prevent fluid from flowing into large gaps, to prevent excessively slow flows that could allow the suspended ice capsules to settle out.  More detailed design is beyond the scope of this paper.

The production module includes 13,122 fabricators plus perhaps 1,000 computer blocks (CPU and memory).  Each block is assumed to be mostly solid diamond.  With 1.6x10^13 production modules, the total volume of "solid" nanoblocks is 2x10^-3 m^3, composed of up to 7.0 kg of diamond.

Walls are required to prevent coolant/solvent fluid from entering the workspace.  The total workspace/fluid wall area of the factory is the sum of the wall areas of each stage.  When stages are stacked together, most faces overlap and need not be filled with walls; the exception is the wall facing the assembly tube.  The wall area of a stage is approximately the area facing each assembly tube plus the area of each tube.  This figure is an over-estimate since it does not account for some of the empty area on each surface facing the gap.  (Note that without walls between adjacent basic modules, blocks can be passed sideways between the modules for increased manufacturing flexibility or decreased need for redundant fabricators.  Although it may save up to 20% of nanofactory mass, this option is not considered further here.)  The program in Appendix A carries out this tedious calculation, computing the total wall area to be about 8400 m^2, plus another 4300 m^2 for the tubes, mostly in the smallest stages.  At 38.2 carbon atoms/nm^2 (Freitas, 1999, Appendix A), the mass of a graphite sheet is 7.6x10^-4 g/m^2.  If the walls are made of graphite sheet, the total interior wall mass is 0.01 kg.  If the walls are made of 20 nm diamond panels, the total interior wall mass is 1 kg.

Because blocks do not need extremely precise alignment, and ridge joints do not require force to assemble, the convergent assembly manipulators do not have to be extremely stiff.  Large-scale manipulators must contend with gravity.  A 5.25-cm diamond cube exerts a force of 5 N; a 15-cm cable capable of lifting it weighs only half a milligram, and the total cable weight scales by 0.5 in each smaller stage.  This analysis breaks down when block forces are dominated by van der Waals attraction (100 nm^2 of van der Waals interface is as strong in tension as 1 nm^2 of diamond), and when the smallest gantry crane component size is limited by manufacturing.  Therefore the total mass of the convergent assembly manipulators is dominated by the total mass of the smallest 0.4-micron units.  Detailed manipulator design is beyond the scope of this paper, but the following analysis shows that manipulator mass will not be a large percentage of factory mass.

The manipulator shown in Figure 3 uses guide rails and linear actuators.  If the smallest possible bulk-diamond cross section for the rails and actuators is 100 nm^2, the volume for four 0.62-micron "Y" rails, two 0.6-micron "X" rails, and one 0.6-micron "Z" rail is 4x10^-4 micron^3.  The factory contains 2.6x10^16 of these manipulators, for a total mass of 0.04 kg.  The 0.8-micron level uses four 1.24 micron "Y" rails, and three 1.8-micron "X" and "Z" rails, for a total volume of 10^-3 micron^3, but there are 1/9 as many manipulators in the factory.  Note that at the 0.4 micron level, the double tripods of the fabricators are exposed and can be used as a 2 DOF manipulator.  Also, the 0.4 micron manipulator may be unnecessary if the 0.8 micron manipulator can sequentially assemble the eight required 0.4 micron sub-blocks before assembling the 0.8 micron block.  (Such an adaptation also saves 10% of module volume.)  A total manipulator mass of 1 kg is surely conservative.

A 10.5-cm product requires an external balloon ~18 cm wide, and larger balloons can be used for larger products (which will require multiple production cycles) or for unfolding small products in a protected environment to avoid joint contamination.  An 18-cm diameter balloon with one-micron walls (to provide UV and physical as well as chemical shielding) requires about half a gram for a 10.5-cm product.  If the factory is shielded from ultraviolet light and air currents, material requirements for the balloon may be substantially reduced.  More sophisticated designs may combine a re-usable UV and structural shield with a much thinner non-reusable chemical shield.

The factory is a rectilinear box; internal vacuum applies bending force to each panel, and each panel applies crushing force to the edge of the adjacent panels.  The casing of the nanofactory must provide support to anchor the interior and prevent the working volume from collapsing under atmospheric pressure.  (Cooling fluid pressure will be contained by the tension members bracing the internal gaps, and will not put additional force on the external casing.)  This can be accomplished with a hollow panel filled with pressurized fluid, with tension members between the panel layers to maintain shape.  The amount of structural material required is essentially independent of the thickness of the panels; 1 cm is chosen for convenience, though additional fluid may be useful as radiation shielding.  Two of the panels are about a square meter each, and are held apart by panels with a sideways area of 1/25 square meter.  This implies that those panels need an internal pressure of 25 atm to resist crushing.  The other panels are about half a square meter, but rest on 2/3 as much sideways area; again, 25 atm is sufficient.  A panel with an internal pressure of 25 atm, internally braced, needs only a slight slant in the bracing to stay flat against a pressure difference of 1 atm.  Closely spaced, thin tension members reduce the required skin thickness to any desired level; 1 micron is assumed here to allow UV shielding and puncture resistance, for a total skin volume of 8x10^-6 m^3.  Sufficient tension members to withstand 25 atm (in one direction) in a total panel volume of 0.03 m^3 requires 1.5x10^-5 m^3.  The total mass of this diamondoid structure is 0.08 kg.

The total nanofactory volume is about half a cubic meter.  Using the conservative estimates, the total mass includes 0.28 kg cooling channel bracing, 7 kg of fabricators and computers, 1 kg interior walls, 1 kg convergent assembly manipulators, and 0.08 kg for exterior shell: total, 9.4 kg of diamondoid.  However, it will likely be possible to save some mass: the convergent assembly manipulators are probably overestimated, the factor of 20 allocated to tension bracing strength and choice of 20 nm walls are probably unnecessary, and the fabricators and computers will contain some empty space.

The maximum distance traveled by power and signal going to the production modules, or blocks coming out, is approximately equal to the length of the assembly tubes of each stage.  This is 1.7 meters.  The total length of all tubes is 1.6x10^8 meters.
 

8.4. Product cycle, duplication, and bootstrapping time

Merkle's assembler (1999) was calculated to require 28 hours to fabricate one billion atoms.  (A 200-nm solid diamond block contains ~1.4 billion atoms.)  However, this was limited by the idiosyncratic requirement to broadcast pressure pulses at 10 MHz through fluid medium to large numbers of assemblers.  Without this requirement, Merkle calculated that the internal mechanisms could work at ten times higher frequency.  This implies a replication time, or product cycle time, of about three hours.  The use of digital logic control allows each actuator (Merkle estimates that the fabricator would use "tens of actuators") to be separately driven sequentially or in concert, eliminating the need for the actuator-selection function and somewhat increasing the speed of operation.  (Merkle stated (personal communication, January 25, 2003) that 1 GHz "should work if you're careful", which implies a product cycle time of about 15 minutes, but this may be overly aggressive.)  Drexler's factory design (1992, chap. 14) used a one-hour replication time, though it assumed the use of more advanced fabrication systems (molecular mills).  Also, many bacteria have a replication time of an hour or less.  In the absence of detailed fabricator designs, a product cycle time estimate of three hours appears to be plausible, though not defensible.

Nanofactory duplication speed is limited by total nanofactory mass.  If the entire mass of the nanofactory were used in active fabricator modules, the factory could duplicate itself in one basic product cycle and double its size in two basic product cycles.  However, the presence of redundant non-operating fabricators, convergent assembly stages, control computers, and inert walls makes this impossible.  The factory can produce 4 kg per product cycle, but will weigh about twice that.  Thus it should be able to produce its mass in two or three product cycles, and during bootstrapping, double its mass in four or five.

Duplication time may also be affected by nanofactory volume.  The volume of the nanofactory is ~300 times that of its product.  However, the nanofactory is mostly empty space, with a density as low as 0.016 g/cm^3.  The nanofactory consists mainly of planes of near-solid nanoblocks (the fabricators and computers); large, flat, thin surfaces (the walls); and linear structures (the convergent assembly manipulators and tensile bracing), so packing density should be quite good.  Note that the densest and most complex structure, the basic production module, occupies only 15% of the factory's volume, and this module itself is mostly empty space.  In fact, 3/4 or more of the total factory mass (the fabricators and computers) occupies only half a percent of the volume.  If the machinery of the fabricator does not require the entire nanoblock volume (and nanoblocks can be made slightly bigger to ensure this), space on top of each fabricator can be reserved for interior structure (gantry cranes) that will be lifted off during unfolding.  This would allow the production module to be fabricated with no wasted volume.  The fact that ridge joints allow rearrangement during unfolding allows bulky components, if any, to be fabricated in flat slices and assembled during unfolding rather than during the convergent assembly stage; such tricks require extra design effort, but can in principle be applied to any extent necessary for compact packing.  It seems quite possible that with careful design of the gathering/assembly tubes and the tension bracing, the factory can be made to unfold from a 3.5-liter volume (produced by three product cycles).

Finally, as discussed in Section 8.5, radiation damage during fabrication will require an extra product cycle: the first convergent assembly operation will take place at the end of the second product cycle, and the final convergent assembly operation will take place after a final, mostly inactive product cycle.

Thus a reasonable estimate is that a nanofactory of this design can duplicate itself in three or four product cycles, and make a factory twice as big in five or six.  To create a nanofactory from a single assembler requires many bootstrapping steps, in which each factory constructs a version with twice the production capacity.  A sufficiently small system (the initial assembler certainly qualifies) will not need redundancy or onboard general-purpose computers.  Thus it will be able to produce a new system with double the production capacity in only two product cycles.  Around the four-micron level, redundancy (see Section 8.5) and computers become necessary.  This is about the size of the machinery in a basic production module.  A minimal bootstrapping recipe has a two-dimensional sheet of fabricators producing a double sheet which then unfolds into a single sheet twice as big.  After 4,096 (2^12) fabricators are produced (12 steps, 24 product cycles), they fabricate a basic production module (3 cycles).  (The smallest devices will require little or no active cooling; see Drexler, 1992, sec. 12.8.)  The full-sized nanofactory contains 2^44 = 1.8x10^13 production modules, requiring 44 additional bootstrapping steps.  Each of these steps requires at least 5 cycles.  The total number of cycles required is ~250-300--if every design works correctly the first time.  With a three-hour cycle time, the minimum cumulative fabrication time required for bootstrapping is ~40 days.
 

8.5. Radiation and failure

Some forms of radiation, such as low-energy alpha particles, create compact swaths of destruction; other forms, such as high-energy electrons and gamma rays, create widely spaced point defects.  The pattern and intensity of damage will depend on the amount of shielding that can be placed around the device; a bootstrapping project could be protected by a lot more shielding than a small product.  Radiation damage also depends on the still-unknown effects of radiation on diamondoid nanomachinery.  Drexler's estimate of radiation damage assumed no shielding.  Because compact swaths of damage rapidly expend the energy of the radioactive particle, such forms of radiation are relatively easy to shield.  Damage rates may be substantially reduced by shielding, which will be especially effective in reducing compact events, but damage from high-energy radiation cannot be eliminated entirely.  The current design assumes that moderate shielding will ensure that radiation damage will occur at widely spaced points.  If this is not the case in practice, redesign to place redundant components beyond the reach of a single swath will be necessary.  Such redesign would complicate the physical layout to some extent, and may impose small speed and power penalties on nanocomputers due to the need to distribute single memory "words" among several nanoblocks, but would not pose a serious problem for the overall design.

If a component has a probability p of survival (not failing), then its failure probability q is 1-p.  A system relying on n non-redundant components will only survive if all its components survive; this probability is p^n.  The failure rate of an n-component system is 1-p^n or 1-(1-q)^n; failure probabilities cannot simply be multiplied.  With q=0.03 for a 1-micron block, the failure rate of a single nanoblock full of sensitive machinery, such as a fabricator, is 0.00024 per year; a 5-micron cube of machinery with no redundancy has a 98% chance of failing during the first year.  n may be treated as a scaling factor rather than an integer: if a system with m (non-redundant) components has a survival rate of p, the survival rate of each component is p^(1/m).  A single nanoblock, 1/125 of a cubic micron, has a 98% chance of lasting a century.  However, a system with 16,000 non-redundant nanoblocks has perhaps a 1% chance of radiation damage in a single day, and 2000 cubic microns (250,000 nanoblocks) has a 15% per day hit rate.  A memory word occupying 3000 cubic nanometers has a chance of being hit of 9x10^-8 per year; the chance of two hits to the same block is the square of that, or 8x10^-15.

The binomial formula gives the probability of exactly x successes in n trials, where each trial has success probability p, as:
n! * [p^x] * [(1-p)^(n-x)] / [x!*(n-x)!] (Weisstein, 2002).
To calculate the probability of at least s successes in n trials, the formula is used repeatedly with values of x from s through n and the results summed. This can be used to compute the probability of at least a minimum required number of redundant components remaining after a certain per-component failure rate.  Because these calculations are extremely tedious and use extremely large numbers, they are not worked out in the text. Appendix A contains a program that calculates the results given in the rest of this section.

Redundancy will be required in a tabletop system full of radiation-sensitive components.  A wide variety of architectural tradeoffs can be used to compensate for the inevitable failure of some percentage of the factory's machinery, but redundant fabricators must be near the components they replace, to allow their products to be substituted.

In theory, it is sufficient to add redundancy only at the lowest level.  The smallest stage produces a 0.4-micron product, and the corresponding unit of failure is a single nanoblock or fabricator.  With no higher-level redundancy, 2^54 ~= 2x10^16 0.4-micron stages must all function reliably to build a 10.5-cm product.  Achieving an aggregate failure rate of 0.03 requires a stage reliability rate of 10^(-7x10^-19) or a failure rate of 2x10^-18.  The failure rate for the unreliable substage is 0.00024; achieving the desired first stage reliability rate requires 5 redundant 0.2-micron fabricators for each 0.4-micron stage, a 63% increase in mass.  However, this analysis is suspect because spatially correlated damage from a single radiation event may wipe out multiple adjacent fabricators.  Since there is no redundancy above the 0.4 micron stage, the loss of a single stage disables the factory.  Additionally, detecting errors in single nanoblocks may require feeling each face of each block, a total of 8.6x10^17 faces or 34,000 square meters.  It may be preferable to defer error checking to higher stages, since the surface area to be checked decreases by a factor of two at each stage while the number of faces decreases by a factor of eight.  If error checking is deferred, some errors will be discovered as a result of failed assembly operations in lower stages; this may eliminate the need for explicit shape checking entirely.  Even if checking is required, the robotics to perform the check will require proportionally less workspace, time, and energy at higher levels.

The cost for single-level redundancy increases rapidly for levels above the lowest.  Redundancy at the 0.8 micron stage means 2x10^15 stages and a substage failure rate of .0019.  The stage reliability rate must be 10^(-7x10^-18) or failure rate of 2x10^-17, which requires 7 redundant substages or an 88% increase in mass.  At the 1.6 micron stage, the substage failure rate is 0.015 and 3x10^14 stages must all remain working for the factory to work.  An overall failure rate of 0.03 requires a reliability per 1.6-micron stage of 10^(-4x10^-17) or failure rate of 10^-16.  This can be achieved with 11 redundant stages in addition to the eight actives, a 238% increase in mass.

A better solution is to implement redundancy in several substages with a scalable design.  If each stage includes nine substages instead of eight, the overall probability of failure decreases at each stage as long as the probability of failure of the sub-stages is less than 3.2% each.  The redundant substage causes a mass increase of 12.5%, and this increase is cumulative; with 19 redundant stages, the factory would increase in mass by 1.125^19 or 9.3 times.  However, most of the stages do not need to be redundant.  The probability of failure increases by a bit less than ten times for each non-redundant stage, but drops off far faster than that for redundant stages with very reliable sub-stages; very approximately, the number of zeros in the failure probability doubles for each redundant stage.  The failure rate of a single nanoblock is about 0.00024 per year.  If the first four stages are redundant, the rest of the stages can be non-redundant.  Implementing this redundancy would increase the fabricator mass of the factory by about 60%.  In fact, with the estimates used here, only the first three stages need to be redundant, but a nanoblock failure rate only twice as high would cause a 7% per year chance of factory failure.  With the first four stages redundant, a factor of ten increase in nanoblock failure rate still provides a yearly factory failure rate of 1 in 10^5; the more conservative design is used.

A redundant stage must either check the input sub-blocks before it attempts to assemble them, or accept that an improperly assembled product (due to sub-stage error) may jam the stage, propagating the unreliability to the higher level.  (A faulty block can usually be pushed back into the faulty substage, clearing the assembly space.)  The only errors that absolutely must be detected are those that will affect convergent assembly at higher levels.  These can be found by feeling each face of each sub-block at whatever stage the errors are to be detected.  Alternatively, if the ridge joints are designed for delayed joining with controllable shims, the mechanical fit may be checked by applying a mating face to the whole surface at once.  If the 400-nm stage is not redundant, then the next four or five stages must be redundant depending on actual error rates.  If both the 0.4-micron and 0.8-micron stages are not redundant, then the next five or six stages must be redundant.  If none of the first three stages is redundant, the 11.5% failure rate of the 1.6 micron stage cannot be reduced by 9-in-8 redundancy.

Once a block is formed correctly, subsequent radiation damage will not prevent convergent assembly; at worst, if a ridge does not expand properly (see Section 3.2.1), the joint will be somewhat weaker than planned.  Once assembled blocks of any size are tested for correct joint function at their surfaces, the larger composite blocks do not need to be tested again; thus, the size at which to test can be selected to maximize overall efficiency.  Above a certain size, robotic hardware can be made tolerant of radiation, and its control computers can be made redundant at insignificant cost.  Fault-tolerant design is therefore unnecessary for assembly machinery above a certain size.  This design assumes that machinery scaled to handle a 3.2 micron sub-block can be made radiation tolerant.  If this is not the case, or if production modules cannot easily be designed to be extremely reliable, additional redundant substages can be added to the branching fractal architecture at any stage.

Radiation damage that occurs during block fabrication, either to the fabricator or the growing nanoblock, will usually cause a malformed or missing block, which must be replaced.  Although only a tiny fraction (~10^-7) of the fabricators will be affected during each product cycle, this still represents ~10^10 failures, which must be dealt with since a nanoblock with the wrong surface configuration could affect the convergent assembly process at a much later stage.  Of course, some percentage of failures will be easily detectable as the fabricator will jam during operation.  In these cases, failure detection will be far easier than failure correction, which is not contemplated in the present design.  Blocks could be tested before assembly simply by running a plate over their surfaces; errors preventing assembly but leaving ridge tops in correct position are unlikely.  (If necessary, a probe could be passed through each of the ridge joint valleys to ensure the absence of blockages.)  Functional damage to the interior of blocks is harder to detect, but need not be detected since it can be treated the same as other radiation-related damage: products (including nanofactories) above a certain scale must be designed to compensate for a certain failure rate.

When damage is detected either during or after fabrication, the faulty fabricator or stage is shut down, and its damaged block is stored permanently in its workspace without blocking other factory operations.  There are several ways to replace the missing block.  The factory could stockpile standard replacement blocks for commonly-used designs, though transferring the block from the stockpile to its proper place in the design would add complexity.  Lacking stockpiled blocks, an adjacent fabricator will have to construct a replacement for each of the failed blocks.  The time penalty to construct the replacement will vary widely depending on product design.  In any product, the number of non-redundant blocks must be small enough to ensure a low failure rate over the life of the product.  This implies that most blocks can be replaced by hollow blocks (to support convergent assembly) that require only a short fabrication time.  A block that is a crucial structural or functional component cannot be replaced by a non-functional version; however, in most cm-scale products, few if any 0.00002-cm blocks will be irreplaceable.  For rapid error recovery in such products, each nanoblock design can be accompanied by a low-mass alternative design permissible for use in a tiny fraction of cases.  In the worst case, a special product cycle would be required to replace the failed blocks; this would have to be done before the convergent assembly of the first cycle's blocks, but could overlap with the second product cycle in products requiring multiple cycles (including duplicate nanofactories).  To prevent further delay from further errors, two replacements for each missing block must be made, one used and the other cached inside the factory or discarded.  The mass of wasted material is roughly equivalent to the mass of fabricators destroyed by background radiation: less than 1% of the factory mass per year.

The nanofactory will contain a wide variety of component sizes, many of them engineered to save mass in order to reduce replication time.  An unusually large number of its nanoblocks may be crucial components that cannot be gutted.  Accordingly, a full additional product cycle is presumed to be necessary in the production of nanofactories.

A low rate of unpredictable error in construction is tolerable as long as it does not disable the nanofactory.  As long as the error rate is not much greater than the damage rate from radiation, a block damaged during fabrication by mechanochemical error may be stored in place, permanently disabling its fabricator.  Drexler has calculated (1992, sec. 6.3) that mechanochemical error rates for many reactions can be significantly lower than radiation error rates.  If the fabricator makes more frequent mechanochemical errors and is not equipped to correct them, the factory will need a mechanism for detecting and discarding failed nanoblocks.

Even if blocks are fabricated correctly, they may still in theory fail to assemble correctly.  An error in block assembly would be likely to jam the nanofactory at a non-redundant stage, so would be unacceptable.  However, the joining process is purely mechanical, and the block faces to be joined are rigid by design.  A suitable pattern of ridge joints can prevent misaligned faces from coming together.  Once blocks are correctly aligned and pushed together, they will be strongly held (relative to the force of gravity and thermal noise) even if the shims do not insert properly.  Accordingly, errors in assembly should occur at a negligible rate.
 

8.6. Cost and difficulty of manufacture

The cost of the nanofactory is comparable to the cost of its product.  The energy cost per kg, including cooling, will probably be less than 250 kWh--less than $20 at current electric rates.  The space required by the nanofactory and its associated cooling equipment is not large and does not need special facilities other than power and a small supply of water to vaporize for efficient cooling.  If exotic feedstock chemistries are not used, the only elements required in bulk are carbon and hydrogen, which are readily available.  The mechanochemical fabricators may require a few atoms of metal apiece as a catalyst, but this will amount to micrograms per kilogram.

Conventional manufacturing encompasses thousands of processes, materials, and components.  This requires multiple factories and much human labor, and involves the transport of intermediate products.  Because a nanofactory can convert simple chemicals into complicated structures and then into final products within a single small enclosure, manufacture will require far less logistical planning.  The simple fabrication, assembly, and error recovery operations contemplated in this design can be completely automated, eliminating labor costs.  The environment of a nanofactory will be small and unspecialized, so the capital and maintenance costs for the environment will be quite low.  A 10.5-cm cube, weighing up to 4 kg, can be manufactured in approximately three hours.  Assuming the feedstock is not overly dangerous, the nanofactory described here would even be appropriate for home use if run at a lower speed to reduce power dissipation requirements.

A 10.5-cm product requires an external balloon ~18 cm wide, and larger balloons can be used for larger products (which will require multiple production cycles) or for unfolding small products in a protected environment to avoid joint contamination.  Because the inflating gas need not be assembled one atom at a time (though it must be perfectly pure), the loss of gas in the released balloon does not contribute significantly to the energy cost of the product.  At $1/liter or more, neon gas (used in Merkle's design) may form a significant fraction of the dollar cost of the product; assuming argon can be substituted without adverse effect, the cost drops to pennies per liter.

It appears, then, that if a cheap feedstock can be found, the costs of products may be determined mainly by the cost of their design and by licensing fees for the use of nanofactory technology.  Design for simple products will require little more than solid-geometry specification.  More complex products will require some work to specify suitable patterns and regions to accommodate the nanoblock system.  However, this should be more than offset by the reduced need to design for a variety of idiosyncratic manufacturing processes.  The reduced cost of prototyping may further reduce design effort and thus cost.  Licensing fees for nanofactory use will be a matter of governmental and economic policy, far beyond the scope of this paper.
 

9. Conclusion and discussion

The nanofactory design is modular and scalable with only two basic plans.  The first is a production module a few microns on a side, which includes a computer and a few thousand fabricators.  The second is the stacking of modules around simple convergent assembly hardware to create larger modules, which can be repeated at least to tabletop size.  Redundancy, heat, control, chemical supply, and convergent assembly mechanisms have been analyzed in some detail.  Products are fabricated in nanoblocks small enough to be made by a single fabricator in a reasonable time, but large enough to contain useful function.  The nanoblock mechanical joining mechanism allows products to be assembled in cubical form by simple robotics and unfolded or rearranged extensively after assembly.  A wide variety of useful products, including duplicate factories, can be made by this system.

The nanofactory design, and detailed plans for bootstrapping, could be completed before the fabricator was finished.  The mechanochemical fabricator design is essentially unmodified from the self-contained fabricator, and the rest of the nanofactory design is entirely mechanical.  The science of mechanics is well established and well understood; simulation can be used with a high degree of confidence to enable design-ahead.  Once the first fabricator becomes available, the nanofactory bootstrap process requires the creation of ~60 different devices, each ~twice as large as the preceding device; however, most of the devices will not require much new engineering or testing, so as soon as a device is created it can attempt to make the next device.  Under plausible assumptions regarding fabricator speed and factory mass, volume, and architecture, the doubling time of a nanofactory is measured in hours, and the entire bootstrap process could in theory take less than 40 days if all of the simulations were reliable, no redesign was necessary, and if every design worked correctly the first time (see Section 8.4).  (The rapid build time allows a debugging cycle more comparable to software engineering than to mechanical engineering.)  Products to be built by the nanofactory can also be partially designed before the factory becomes available.

It has been argued that molecular nanotechnology will not create a sudden disruption in technological capability because of the need for testing each new product and technique (Kaehler, 1996).  However, the present analysis casts doubt on this position.  Although the current paper does not speak to the difficulty of creating a mechanochemical fabricator, it does indicate that the time interval from the first fabricator to a programmable nanofactory could be quite short.  It also appears that the nanoblock design paradigm is an effective method of reducing design and assembly difficulty while retaining product complexity and functionality: the use of a few standard nanoblock types can allow easy design and even predesign of a wide variety of products.

Once a self-contained, reasonably inexpensive nanofactory is produced, it can be rapidly duplicated and used widely.  A power use of 250 kWh/kg means that a large 1-GW power plant, or four square miles of sun-collecting surface, could produce ~12,000 8-kg nanofactories per day (not including feedstock production).  If feedstock is sufficiently easy to produce, sufficient factories to supply the world's population could be produced in a few months.  Without knowing the design for the initial fabricator, it is impossible to estimate the cost or availability of the feedstock chemicals.  However, for applications such as computers and some medical, aerospace, military, and surveillance hardware, the output of a nanofactory would be economically and/or technologically competitive at almost any price; also, the nanofactory might be used to build compact, automated "lab on a chip" chemical processing plants, reducing the feedstock price.

The wide range of useful products that can be produced by even a basic nanofactory argues strongly for its commercial viability, its humanitarian potential, and its military significance.  The apparent feasibility and simplicity of integrating mechanochemical fabricators into a nanofactory indicates that development of an assembler may therefore be an event of substantial political, military, and economic significance.  It also indicates that any project to create an assembler should include a parallel project to bootstrap that assembler into a nanofactory; the additional effort required will probably be a fraction of the assembler design and creation effort.

This paper has analyzed a simple, scalable design leading to a functional meter-scale nanofactory and suggesting the possibility of rapid bootstrapping from primitive mechanochemical diamondoid fabricators.  The particular design described here appears likely to be practicable and accessible to present-day engineering practice.  Little attempt was made in this design to save mass, time, or energy; it is possible that with further engineering effort, the first nanofactory might be significantly more efficient in each of these categories.  The design is highly scalable, with only one basic architecture change at the few-micron scale, and can be bootstrapped from a single fabricator.  Most of the design can be simulated in detail, and most of the techniques and mechanisms tested by experiment, before the fabricator becomes available.  This indicates the possibility of rapid development from a basic mechanochemical fabricator to a flood of advanced products.
 

Appendix A. Calculations in software

....
If 2^54 0.4-micron stages all have to work, each stage needs
  a failure rate of 1.69x10^-18
That requires substage redundancy of 5 (plus the 8 required)
....
If the first three stages are 9-in-8 redundant [1,1,1,0,0,0...]
  The chance of factory failure is 2.73x10^-4
....
Small cooling gap volume = 4.673892e-003 m^3
Level 1, width 3.63e-005 height 1.62e-005 depth 2.54e-005 product size 3.2e-006
  4.39805e+012 stages, volume of tube 0.00138414, surface of tube 1392.74
  Volume of gap 4.986e-003 m^3, surface area of gap 2.289e+003
....
Pressure for 2048 blocks is 564378 Pa (5.6 atm), flow 0.008325 m/s
....

These numbers are used in Section 8.  The complete printout is included at the beginning of the program file.
 

Appendix B. Projections from the Merkle assembler

B.1. Mechanochemical baseline

Although the assembler is not fully specified, either chemically or mechanically, we can draw quite a few conclusions about its makeup.  Merkle does not provide a list of the chemicals, or even the elements, required to make his assembler.  However, we can safely assume that the elements include carbon and hydrogen.  Chemical structures specifically mentioned in the paper include a large graphite tube, polyyne rods in small (9,0) buckytube sheaths (Merkle, 1997b), and diamond.  It is safe to assume that the diamond can be made in a variety of shapes necessary for the double tripod and other equipment, probably including hollow beams, concave parts, and overhangs.  Since half a billion atoms cannot be specified manually, the majority of the chemical steps required to make a range of diamond shapes must be determined by computer program.  (This is plausible since diamond lattice is repetitive.)

Since half a billion mechanochemical operations also cannot be tested individually, we may assume that the required computer-controlled mechanochemical operations usually work as desired.  In other words, within some presently unknown limits, specification of a volume can reliably result in its being filled with diamond lattice.  Given the design complexity of the assembler, it is likely that the assembler design process will result in a fairly broad array of known-good diamond shape configurations.  Note that this does not require a full understanding of the limits of automated diamondoid chemistry.  It is likely, and will be assumed for the purposes of the present analysis, that proposed diamond shapes can be approved or disapproved without requiring physical testing or detailed simulation of their construction.  Since the assembler design almost certainly involves a variety of passivated surfaces, it may be assumed that diamond surfaces and graphite edges may be passivated by automated design.

Friction between interfaces may vary by orders of magnitude depending on the detailed surface characteristics.  (Drexler, 1992, chap. 10) and (Merkle, 1993) have shown that it should be possible to design sliding interfaces with no static friction and low dynamic friction.  Drexler analyzes several simple surfaces, compatible with diamond lattice, that should have these characteristics.  It will be assumed that semi-automated bulk diamond design is compatible with use of such surfaces for planar sliding interfaces.
 

B.2. Chemistry, electronics, and mechanics

Although the mechanics are not completely specified, there are certain devices that must be available for a fabricator design to work.  In addition to the polyyne/buckytube sheathed control cables, a double tripod design requires universal joints, rotating joints with one and two degrees of freedom, at least one threaded joint, and sliding joints.  Ratchet drive mechanisms must include springs and interlocking parts.  Rotating joints may pose special difficulty in design and construction, because of the need for low potential energy slopes at every angular position, but the nanofactory does not require a large set of small rotating joints; most motion (e.g. rod logic) will be linear.  Above a certain size, a roughly cylindrical diamond shape or void can be sheathed or lined with multiple layers of graphite (buckytubes), creating a circular and slippery cross-section.

An assembler must contain many parts that are not bonded to each other and therefore would not be well supported if manufactured in place; this requires some capacity for fabricating two parts and then moving them into conjunction.  This further implies that a variety of completed shapes can be picked up and then released by the double tripod.

A large number of diamondoid devices, including several useful classes of mechanism such as bearings, rely on strained bonds.  These bonds can be formed either during mechanochemical fabrication, or as a result of assembly.  Strained bonds formed mechanochemically may require specialized manipulation, individually designed for each part.  Strained bonds formed during assembly are the result of mechanical bending operations; a simple example is bending a straight diamond rod and joining the ends to form a hoop (Drexler, 1992, sec. 11.3.2).  The nanofactory design probably does not require parts requiring mechanochemically strained bonds except for specific designs already present in the assembler. Sufficiently large buckytubes collapse naturally due to van der Waals force, providing a flat and unstrained work area, so are essentially equivalent to graphite.
 

B.3. Mechanochemical error rate

Acknowledgements

References

Algor, Inc. (2003). Professional MEMS Simulation. Retrieved July 24, 2003 from http://www.algor.com/products/Profes1511/default.asp

Bishop, F. (1996). A Description of a Universal Assembler. Proceedings of the 1996 IEEE International Joint Symposia on Intelligence and Systems (IJSIS '96), 126.  Retrieved July 24, 2003 from http://www.iase.cc/html/universal.htm

Blaze Network Products. (2003). Manufacturing Technology. Retrieved July 24, 2003 from http://www.blazenp.com/technology/manufacturing.html

Bradbury, R. J. (2003). Protein Based Assembly of Nanoscale Parts. Retrieved July 24, 2003 from http://www.aeiveos.com/~bradbury/Papers/PBAoNP.html

Cagin, T., Jaramillo-Botero, A., Gao, G., & Goddard, W.A., III. (1998). Molecular mechanics and molecular dynamics analysis of Drexler-Merkle gears and neon pump.  Nanotechnology 9(3), 143-152. Retrieved July 24, 2003 from http://www.wag.caltech.edu/foresight/foresight_1.html

Drexler, K. E. (1986). Molecular Engineering :Assemblers and Future Space Hardware. Proceedings of the 33rd Annual Meeting of the American Astronautical Society, 86-415 1327-1332. Retrieved July 24, 2003 from http://www.aeiveos.com/~bradbury/Authors/Engineering/Drexler-KE/MEAaFSH.html

Drexler, K. E. (1992). Nanosystems. New York: John Wiley & Sons.

Freitas, R. A., Jr. (1999). Nanomedicine Volume 1. Georgetown, TX: Landes Bioscience. Retrieved July 24, 2003 from http://www.nanomedicine.com

Freitas, R. A., Jr., & Merkle, R. C. (in press). Kinematic Self-Replicating Machines. Georgetown, TX: Landes Bioscience.  [Not yet available]: http://www.MolecularAssembler.com

GE Advanced Ceramics. (2002). Graphite Monochromators. Retrieved July 24, 2003 from http://www.advceramics.com/acc/products/graphite_monochromators/

Groening, O., Kuttel O. M., Emmenegger, C. H., Groening, P., & Schlapbach, G. L. (2003). Field emission properties of nanocarbon structures. Switzerland: University of Fribourg, Physics Department. Retrieved July 24, 2003 from http://www.fondazione-elba.org/28.htm

Handbook of Chemistry and Physics (51st ed.). (1971). Cleveland, OH: The Chemical Rubber Co.

Hall, J. S. (1993). Utility Fog: A Universal Physical Substance. Vision-21, Westlake, OH; NASA Conference Publication 10129, 115-126 Retrieved July 24, 2003 from http://www.aeiveos.com/~bradbury/Authors/Computing/Hall-JS/UFAUPS.html

Hall, J. S. (1999). Architectural Considerations for Self-replicating Manufacturing Systems. Nanotechnology, 10, 323-330. Retrieved July 24, 2003 from http://www.foresight.org/Conferences/MNT6/Papers/Hall/index.html

Halfhill, T. R. (1993, May). Intel Launches Rocket in a Socket. Byte, 92-108.

Hla, S., Bartels, L., Meyer, G., & Rieder, K. (2000). Inducing All Steps of a Chemical Reaction with the Scanning Tunneling Microscope Tip: Towards Single Molecule Engineering.  Phys. Rev. Lett., 85, 13, 2777-2780. Summary retrieved July 24, 2003 from http://www.aip.org/enews/physnews/2000/split/pnu503-2.htm

Ipe Nanotube Primer. (2001). Fabrication of single nanotube emitters. Retrieved July 24, 2003 from http://ipewww.epfl.ch/gr_buttet/Manips/Nanotubes/NTfieldemission3.htm

Intracel LTD. (2001). Model P2000 Laser Based Puller. Retrieved July 24, 2003 from http://www.intracel.co.uk/suttp2000.htm

Kaehler, T. (1990). Molecular Carpentry. Foresight Update 10. Palo Alto, CA: The Foresight Institute. Retrieved July 24, 2003 from http://www.foresight.org/Updates/Update10/Update10.3.html

Kaehler, T. (1996). In-Vivo Nanoscope and the Two-Week Revolution. In B. C. Crandall (Ed.), Nanotechnology. Boston: MIT Press.

Kozierok, C. M. (2001). ECC [Error Correction Code]. The PC Guide. Retrieved July 30, 2003 from http://www.pcguide.com/ref/ram/errECC-c.html

Merkle, R. C. (1993). A Proof about Molecular Bearings. Nanotechnology, 4, 86-90. Retrieved July 24, 2003 from http://www.zyvex.com/nanotech/bearingProof.html

Merkle, R. C. (1997a). Convergent assembly. Nanotechnology, 8(1), 18-22. Retrieved July 24, 2003 from http://www.zyvex.com/nanotech/convergent.html

Merkle, R. C. (1997b). Binding sites for use in a simple assembler. Nanotechnology, 8(1), 23-28. Retrieved July 24, 2003 from http://www.zyvex.com/nanotech/bindingSites.html

Merkle, R. C. (1997c). A New Family of Six Degree of Freedom Positional Devices. Nanotechnology, 8(2), 47-52. Retrieved July 24, 2003 from http://www.zyvex.com/nanotech/6dof.html

Merkle, R. C. (1997d). A proposed metabolism for a hydrocarbon assembler. Nanotechnology, 8(4), 149-162. Retrieved July 24, 2003 from http://www.zyvex.com/nanotech/hydroCarbonMetabolism.html

Merkle, R. C. (1998). Theoretical studies of diamond mechanosynthesis reactions. Nanotechnology, 9, 285-296. Retrieved July 24, 2003 from http://www.zyvex.com/nanotech/mechanosynthesis.html

Merkle, R. C. (1999). Casing an assembler. Nanotechnology, 10, 315-322.  Retrieved July 24, 2003 from http://www.zyvex.com/nanotech/casing.html

Merkle, R. C. & Freitas, R. A., Jr. (2003). Theoretical analysis of a carbon-carbon dimer placement tool for diamond mechanosynthesis. J. Nanosci. Nanotechnol. 3, 1-6. Retrieved July 24, 2003 from http://www.rfreitas.com/Nano/DimerTool.htm

MinFeng, Y., Mark J. D., Skidmore, G. D., Henry W. R., XueKun, L., Ausman, K. D., Von Ehr, J. R., & Ruoff, R. S. (1998). 3 Dimensional Manipulation of Carbon Nanotubes under a Scanning Electron Microscope. Draft paper for a talk at the Sixth Foresight Conference on Molecular Nanotechnology. November 12-15, Santa Clara, CA. Retrieved July 24, 2003 from http://www.zyvex.com/Research/Publications/papers/Foresight98.html

Morrison, M. (2002). Breakthrough Compression Technology for the Semiconductor Industry - GDSII and MEBES Formats. SolutionSoftSystems Inc. Retrieved July 24, 2003 from http://www.solution-soft.com/gds_mebes_compressors.shtml

Nowicki, A. (2003). Structural Materials. Earth to Orbit Transportation Bibliography. Retrieved July 24, 2003 from http://www.islandone.org/LEOBiblio/SPBI1MA.HTM

Olson, S. (2002). Interview with Scott Mize. NanoMagazine.com. Retrieved July 24, 2003 from http://www.nanomagazine.com/2002_08_16

Optics.org. (2001). Diamond LED Sparks Laser Hopes. Retrieved July 24, 2003 from http://optics.org/articles/news/7/6/15/1

Oyabu, N., Custance, O., Yi, I., Sugawara, Y., & Morita, S. (2003). Mechanical vertical manipulation of selected single atoms by soft nanoindentation using a near contact atomic force microscope. Phys. Rev. Lett., 90, 176102.  Summary retrieved July 24, 2003 from http://focus.aps.org/story/v11/st19

Popovich, K. (2002). Intel Rolls Out Mobile Pentium 4 Chip. eWeek. Retrieved July 24, 2003 from http://www.eweek.com/article2/0,3959,73697,00.asp

Salisbury, D. F. (2001). Turning diamond film into solar cells. Exploration. Retrieved July 24, 2003 from http://exploration.vanderbilt.edu/news/news_diamond.htm

Sinnott, S. B, Colton R. J, White, C. T,. Shenderova O. A,  Brenner, D. W., & Harrison, J. A. (1997). Atomistic simulations of the nanometer-scale indentation of amorphous-carbon thin films. American Vacuum Society. Retrieved July 30, 2003 from  http://pyramid.spd.louisville.edu/~eri/papers_pres/sinn6.pdf

Sullivan, J. P. (2002). Amorphous Diamond for MEMS. Paper presented at the American Physical Society, Indiana Convention Center. Abstract retrieved July 25, 2003 from http://www.eps.org/aps/meet/MAR02/baps/abs/S3280005.html

Telling, R. H., Pickard, C. J., Payne, M. C., & Field, J. E. (2000). Theoretical Strength and Cleavage of Diamond. Physical Review Letters, 84(22), 5160-63. Retrieved July 25, 2003 from http://www.tcm.phy.cam.ac.uk/~cjp20/publications/PRL84_5160.pdf

TOP500.Org. (2002). Top500 Computer Sites: Earth Simulator. Retrieved July 25, 2003 from http://www.top500.org/top5/2002/11/one/

Tunkel, R. N. (2002).  DPZT_flow. Retrieved July 25, 2003 from http://www.geocities.com/invitation21/DPZT_flow.htm

Weisstein, E. (2002).  CRC Concise Encyclopedia of Mathematics, 2nd. ed. Boca Raton, FL: CRC Press.

Whitney, D. E., Peschard, G., & Artzner, D. (1998). Voices from Engine Plants. MIT International Motor Vehicle Program. Retrieved July 25, 2003 from  http://web.mit.edu/ctpid/www/Whitney/morepapers/voices.pdf

World Factbook 2002. (2002). Central Intelligence Agency (editor). Retrieved July 25, 2003 from http://www.cia.gov/cia/publications/factbook/print/us.html